http://nyhederne.tv2.dk/2015-03-13-jaegersoldat-fordoblede-54-svage-elevers-karakterer-paa-fire-uger

Torsdag aften afsluttede de første 54 9. klasseelever det lynkursus, som Odense Kommune har købt til dem. Resultaterne efter den såkaldte Basecamp 15 er opsigtsvækkende.
I stavning har eleverne i gennemsnit rykket sig fra karakteren 1,7 til 3,87. I læsning er karakteren gået fra 1,37 til 5,75, mens eleverne har flyttet sig fra 3,5 til 7,9 i matematik.
Militærmand står bag
Manden bag kurserne er den tidligere jægersoldat Nicolai Moltke Leth. Han mener, at det er en kombination af flere ting, der gør, at de unge er i stand til at rykke sig så meget på så kort tid.
– Det er en markant fremgang, vi har set. Det skyldes en blanding af arbejde med de bedste faglige værktøjer og samtidig arbejde med de personlige og sociale kompetencer. Det gør, at de unge kommer til at tro på sig selv, så de kan optage faglig læring, forklarer Nicolai Moltke Leth til DR Fyn.
Der går nogle måneder, inden de unge får test, om kurset så også kan bære, når de skal til afgangseksamen i maj og juni. Indtil da får de unge tilknyttet en mentor, som skal hjælpe dem med at holde de gode takter fra kurset.

Men fænomenet kan også forklares rent statistisk. På engelsk hedder det regression towards the mean (selvfølgelig opdaget af Galton!). Det skyldes at når man laver en måling som ikke har perfekt pålidelighed (dvs. man måler ikke det man gerne vil helt perfekt), og man så udvælger en gruppe baseret på datapunkternes ekstremitet (dvs. de ligger langt fra middel, højt eller lavt), så skyldes en del af deres ekstremitet en tilfældighed. Siden tilfældigheder per definition ikke har nogen sammenhæng med noget andet, så betyder det at hvis man laver en ny måling af samme ting (i skolekarakterer i dette tilfælde), så vil de meget stor sandsynlighed ikke være lige så lave/høje som før. De vil ‘gå mod midten’ fordi at en del af deres lavhed/højhed skyldes en tilfældighed.

Simulering

Vi kan lave en simulering for at vise princippet. Jeg har gjort dette:

1. Genereret 100 tilfældige normalfordelte tal. Dette er vores rigtige scorer (true scores), som vi ikke kan måle direkte fordi vores målemetode er fejlbehæftet.
2. Lavet en måling af disse tal hvor jeg har introduceret fejl i målingen.
3. Lavet en anden måling af disse tal hvor jeg har introduceret fejl i målingen.
4. Rangeret alle scorerne således at de får et tal fra 1 til 100.
5. Udregnet forbedringen fra første til anden måling.

Vi kan nu se en illustration af regression mode middel:

Tallene på x-aksen er personens relative placering ved første måling. Tallene på y-aksen er personens forbedring ved anden måling ifht. første måling. Vi ser således en sammenhæng: de personer som klarede sig godt i første måling klarerede sig relative ringere ved anden måling (deres forbedringsværdier er negative, de er rykket ned i den relative placering), mens de personer som klarede sig relativt skidt ved første måling klarede sig relativt bedre ved anden måling (deres forbedringsværdier er positive, de er rykket op i den relative placering). Den røde linje viser den lineære sammenhæng (OLS regression, r=.38). Tallet ved hver prik viser personens placering ved anden måling. Vi kan således se nogle ret store forbedringer hos nogle personer. Personen som lå nr. 1 ved første måling ligger kun nr. 43 ved anden måling (42 pladser ned). Mens at personen som lå nr. 99 ved første måling ligger nr. 63 (36 pladser op) ved anden måling.

Hvis vi vender tilbage til karakterer, så vil man se samme mønster. Meningen med karakterer i et fag er at de skal afspejle personens evne i det fag. Men alle er enige om at karakterer ikke afspejler personeners evner perfekt. I min data er sammenhængen mellem karakterer og personernes rigtige evner r=.81-.82 (første og anden måling). Man måler altså en del forkert når man måler folks evner i et skolefag ved en eksamen. Laver man to målinger, vil disse begge indeholde en del målefejl, men den vil generelt være forskellig fra måling til måling. (Her ignorerer vi at nogle personer er bedre til at gå til eksamen end andre hvilket gør diskussionen mere kompliceret.). Hvis vi ser på sammenhængen mellem vores to målinger så er den .71, hvilket er kendt som test-retest pålideligheden. Jeg har i mit eksempel forsøgt at vælge en realistisk værdi for skolekarakterer. Jeg kunne ikke finde et udgivet tal, så jeg har lavet et gæt.

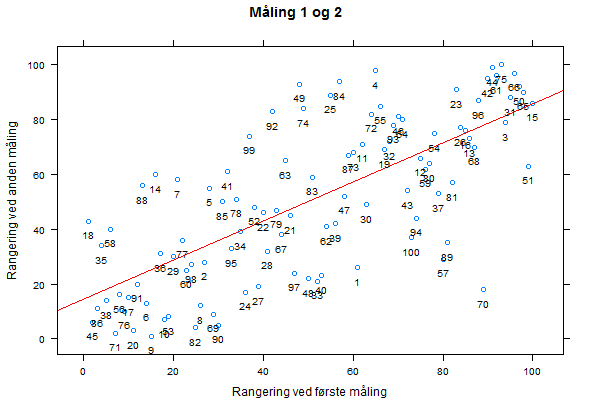
Vi kan også plotte måling 1 og 2:

Fortolkning af data

Regression mod middel-effekten betyder således at man skal være lidt mere varsom med at fortolke kausalitet ud fra data som er selekteret på at score særlig ekstremt. I tilfælde med Odenses jægerkursus, så er eleverne til jægerkurset nok særligt udvalgt fordi at de klarede sig ringe til afgangsprøven. Pga. regression mod middel ville man således forvente at disse elever ville klare sig relativt bedre hvis de tog eksamen igen — helt uden at jægerkurset havde nogen effekt. En forbedring kan således ikke tilskrives jægerkurset alene. Hvis man ville finde ud af hvor meget jægerkurset hjælper, bliver man nødt til at lave et randomiseret kontrolleret forsøg: inddele nogle elever i to grupper tilfældigt (vigtigt!), give den ene gruppe jægerkurset og den anden ingenting. Test derefter begge grupper igen. Forskellen skyldes noget som har med jægerkurset at gøre.

Disse ting er værd at overveje før at man bruger store summer penge på kurser som måske slet ikke har en effekt, eller kun har en ringe effekt.

I øvrigt er det nonsens at sige, at snakke om fordobling i karakterer da karakterskalaen ikke er en ratiomåling.

Datatabel

Tabellen nedenunder indeholder de tilfældige tal jeg brugte. Hvis du kører min kode får du nogle andre tal, men generelt vil du se noget lign.

Person#	Rigtig placering	Rangering ved måling 1	Rangering ved måling 2	Forbedring
18	3	1	43	-42
45	8	2	6	-4
86	6	3	11	-8
35	10	4	34	-30
38	15	5	14	-9
58	11	6	40	-34
71	7	7	2	5
56	24	8	16	-8
76	9	9	10	-1
17	28	10	15	-5
20	4	11	3	8
91	13	12	20	-8
88	30	13	56	-43
6	1	14	13	1
9	2	15	1	14
14	19	16	60	-44
36	17	17	31	-14
10	16	18	7	11
53	14	19	8	11
29	29	20	30	-10
7	18	21	58	-37
77	21	22	36	-14
60	31	23	25	-2
98	27	24	27	-3
82	5	25	4	21
8	20	26	12	14
2	12	27	28	-1
5	53	28	55	-27
69	25	29	9	20
90	34	30	5	25
85	33	31	50	-19
41	75	32	61	-29
95	22	33	33	0
78	54	34	51	-17
34	49	35	39	-4
24	50	36	17	19
99	58	37	74	-37
52	26	38	48	-10
27	46	39	19	20
22	73	40	46	-6
28	62	41	32	9
92	86	42	83	-41
79	23	43	47	-4
67	36	44	38	6
63	74	45	65	-20
21	56	46	45	1
97	37	47	24	23
49	87	48	93	-45
74	64	49	84	-35
48	39	50	22	28
83	68	51	59	-8
33	41	52	21	31
40	42	53	23	30
62	82	54	41	13
25	69	55	89	-34
39	71	56	42	14
84	89	57	94	-37
47	40	58	52	6
87	38	59	67	-8
73	45	60	68	-8
1	52	61	26	35
11	77	62	71	-9
30	80	63	49	14
72	72	64	82	-18
4	99	65	98	-33
55	44	66	85	-19
19	59	67	69	-2
32	85	68	72	-4
93	65	69	78	-9
46	93	70	81	-11
64	60	71	80	-9
43	70	72	54	18
100	48	73	37	36
94	35	74	44	30
12	63	75	66	9
59	66	76	62	14
80	67	77	64	13
54	83	78	75	3
37	55	79	53	26
57	32	80	29	51
89	57	81	35	46
81	43	82	57	25
23	76	83	91	-8
26	84	84	77	7
16	61	85	76	9
13	81	86	73	13
68	51	87	70	17
96	95	88	87	1
70	47	89	18	71
42	88	90	95	-5
44	90	91	99	-8
61	94	92	96	-4
75	100	93	100	-7
3	92	94	79	15
31	97	95	88	7
66	91	96	97	-1
50	79	97	92	5
65	96	98	90	8
51	78	99	63	36
15	98	100	86	14

R kode

Koden er skrevet i R. R er et gratis statistiksprog som er relativt nemt at bruge.

#Regression towards the mean
true.scores = rnorm(100) #100 normal datapoints
measurement.1 = true.scores+.7*rnorm(100) #measure, with .1 error introduced
measurement.2 = true.scores+.7*rnorm(100) #measure again, with .1 error introduced

data = cbind(true.scores,measurement.1,measurement.2) #data
round(cor(data),2) #correlations

rank.true = rank(true.scores) #rank data
rank.1 = rank(measurement.1) #
rank.2 = rank(measurement.2) #

data.rank = data.frame(cbind(rank.true,rank.1,rank.2)) #rank data
data.rank["improvement"] = rank.1-rank.2
data.rank = data.rank[order(data.rank[,2]),] #order data by measurement 1

library("lattice")

xyplot(improvement ~ rank.1, data.rank, type=c("p","r"),col.line ="red",
       xlab="Rangering ved første måling",ylab="Forbedring på anden måling",main="Regression mod middel",
       panel=function(x, y, ...) {
         panel.xyplot(x, y, ...);
         ltext(x=x, y=y, labels=data.rank[,"rank.2"], pos=1, offset=1, cex=0.8)
       })
xyplot(rank.2 ~ rank.1, data.rank, type=c("p","r"),col.line ="red",
       xlab="Rangering ved første måling",ylab="Rangering ved anden måling",main="Måling 1 og 2",
       panel=function(x, y, ...) {
         panel.xyplot(x, y, ...);
         ltext(x=x, y=y, labels=rownames(data.rank), pos=1, offset=1, cex=0.8)
       })