Some games involve chance elements. We can theoretically distinguish between a few types of chance elements. First, the simplest, are direct chance elements as in rolling dice, flipping a coin, or shuffling cards. Ideally, they are purely random (like atmospheric noise), but in practice they are implemented via one of the above methods (which are not entirely random, but random enough for humans). Second, chance in the sense of imperfect information. This can work in someone’s favor. If we play a real time strategy (RTS) game with fog of war (limited map visibility), and I send my attacking units to the only part of your base that wasn’t defended when I had no way to know that, that was lucky on my part and unlucky on your part. There is no dice chance event here, all the actions were under both players’ control, it just so happened due to lack of knowledge that I got lucky and attacked the part of the base that wasn’t defended. Third, matters of performance or execution of a given action. When I play table tennis and aim for the corner of your side of the table. Strictly speaking, there is no metaphysical randomness here. The movement of my hand and the ball is essentially entirely deterministic following classical mechanics. However, we still refer to a particular good hit as a lucky shot. We can refer to these three types of chance or luck elements as dice luck, ignorance luck, and performance luck. Having good luck means a chance element that favors oneself over the other player(s).
With these in mind, we can measure or rate games on their relative importance of skill vs. luck in deciding who wins. There are some games that have essentially no skill in them, such as tossing coins,or war (the card game). On the other hand, there are games that have no random elements in the first two meanings above, like Chess or Tic Tac Toe (3 in a row). These are games of perfect information, no dice throws etc. (In Chess, if you play only a single game, then white has an advantage, and who is white might be down to a coin flip, introducing some luck. But in serious play, they balance the games with equal numbers of games as white and black to remove this chance element.) Every other game is somewhere in between these two extremes, but where exactly? A game of Backgammon involves more chance (because dice) than does a typical RTS like Starcraft 2, but how much exactly?
There is some academic research into this. I was able to find this particularly nice paper:
- Duersch, P., Lambrecht, M., & Oechssler, J. (2020). Measuring skill and chance in games. European Economic Review, 127, 103472.
Our method can be described in two steps. First, we propose a measure for skill and chance in games. Then, we use this measure to define a 50%-benchmark. For the first step, rather than using performance measures like prize money won or finishing in the top x percentile in a tournament, we apply a complete rating system for all players in our datasets. In particular, we build on the Elo-system (Elo, 1978) used traditionally in chess and other competitions (e.g. Go, table tennis, scrabble, eSports). It has the advantage that players’ ratings are adjusted not only depending on the outcome itself, but also on the strength of their opponents. Additionally, it is able to incorporate learning. The rating system is applicable to two player games immediately, and can be generalized to handle multiplayer competitions. We calibrate the Elo rating system to obtain a best fit for each game and type of competition individually.
In the Elo rating, a given difference in ratings of two players corresponds directly to the winning probabilities when the two players are matched against each other. Thus, the more heterogeneous the ratings are, the better we can predict the winner of a match. If the distribution of Elo ratings is very narrow, then even the best players are not predicted to have a winning probability much higher than 50%. The wider the distribution, the more likely are highly ranked players to win when playing against lowly ranked players, and the more heterogeneous are the player strengths. In our data, the rating distributions of all games are unimodal, which makes it possible to interpret the standard deviation of ratings as a measure of skill. Accordingly, the standard deviation is high in games of pure skill and with a large heterogeneity of playing strength (e.g. chess). On the other hand, if the outcome of a game is entirely dependent on chance, in the long run, all players will exhibit the same performance. In this case, the standard deviation of ratings tends to zero.
In the second step, we propose an explicit 50%-benchmark for skill versus luck. We do this by constructing a hybrid game that is arguably exactly half pure chance and half pure skill. For the pure skill part we use chess as a widely accepted game of skill with the added benefit that there is an abundance of chess data. We construct our hybrid game by randomly replacing 50% of matches in the chess dataset by coin flips. This way, we mix chess with a game that is 100% chance and thereby construct what we call “50%-chess”. We can then compare the standard deviations of ratings for all of our games to 50%-chess as a benchmark.
One may argue that even chess contains an element of chance. For comparison, we also provide a more extreme bench- mark. This “50%-deterministic” game consists of matches where the better player wins 50% of the matches right away, while the other 50% are decided by chance.
Applying our method to the data, we obtain a distribution of ratings for each game. As expected, chess and Go, as well as a traditional sport like tennis, have high standard deviations. Poker, on the other hand, has one of the narrowest distributions of all games. When we compare the games to our benchmarks, we find that poker, backgammon, and other popular online games are below the threshold of 50%-chess (and therefore also below the higher threshold of 50%-deterministic) and thus depend predominantly on chance. In fact, when we reverse our procedure and ask how much chance we have to inject into chess to make the resulting distribution similar to that of poker, we find that poker contains about as much skill as chess when 75% of the chess results are replaced by a coin flip. Furthermore, the amount of skill we find in poker is comparable to that of a deterministic game when 85% of the results are replaced by chance.
Their results based on analyzing large datasets of games:
They explain:
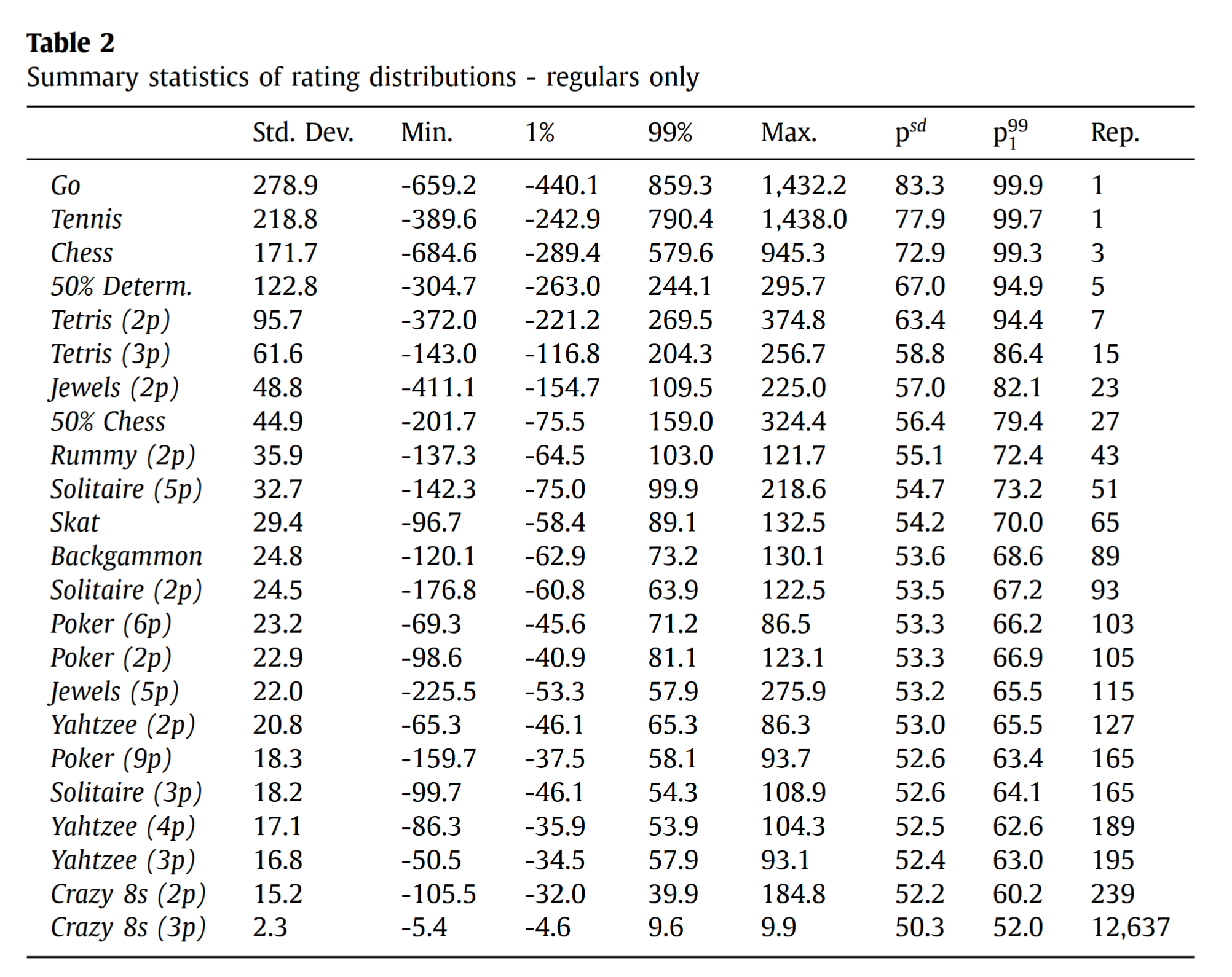
In Table 2 we report summary statistics for the Elo rating distributions of regular players. These include the minimum and maximum rating, the rating of the 1% and the 99% percentile player, and most importantly, the standard deviation of all ratings. We sort the table according to this value. Via formula (1), we can transform the standard deviation of each game into the corresponding winning probability of a player who is exactly one standard deviation better than his opponent. We refer to this probability as psd . For comparison, we also provide the winning probablities when a 99% percentile player is matched against a 1% percentile player, which we call p99 1 . The winning probability psd can be used to calculate the number of matches necessary so that a player who is one standard deviation better than his opponent wins more than half of the matches with a probability larger than 75%.25 This number is reported in the repetitions column (abbreviated “Rep.”).
Thus, some quite popular games involve large amounts of luck. A top 1% player almost never loses to a bottom 1% player in tennis (0.3% of the time). In fact, in real life these losses are probably due to injuries or the like. But in 2 player Poker, a top player losing to a bottom player happens a lot, about 33% of the time according to the model. Poker thus involves rather large amounts of luck.
Ideally, we would have a ranking of all games by this same metric, but since I didn’t have time to try to download a large collection of game histories for every game (which might involve difficult web scraping), I settled on a different approach: asking people to estimate the roles of skill vs. luck. Asking people may seem stupid, but Francis Galton showed back in 1907 (Vox populi) that this can work very well for certain estimation tasks:
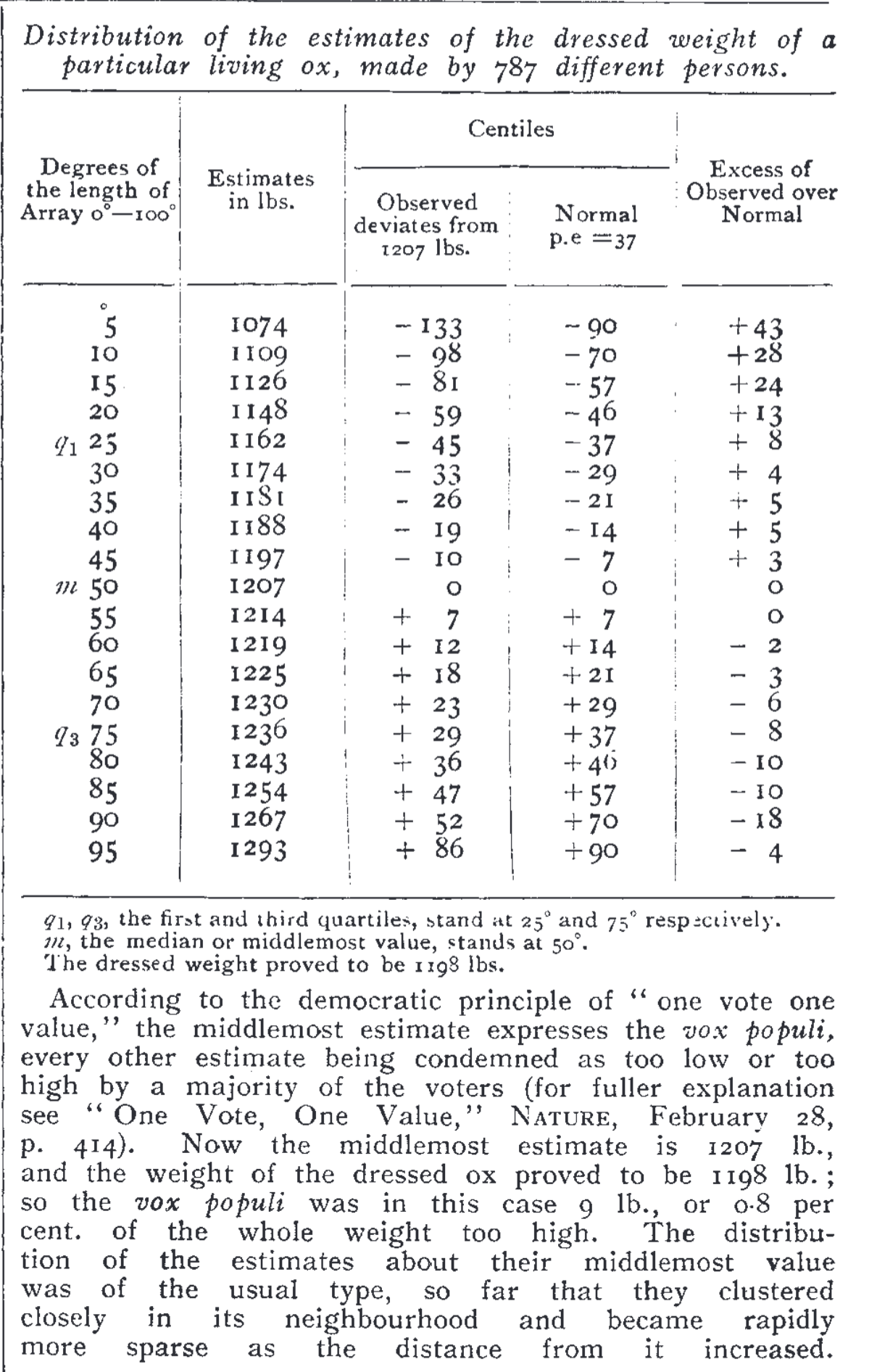
In his study, 787 people tried to guess the weight of a ox at a fair. They had incentive to get this right because there was a small entrance fee and a prize for the closest guess. The median guess turns out to be within 1% of the true value when the ox was weighed. In fact, that’s probably within the error of the scale used too.
The assumptions for a survey estimate to work are that 1) the errors for each person are independent (i.e., they can’t see each other’s votes or be influenced by the same biases), and 2) that people have no systemic biases. In an online survey of games’ ranking importance of skill vs. luck, the first is approximately satisfied, as voters couldn’t see the results before voting. Furthermore, with regards to the second assumption, they have no particular incentive to be untruthful as it’s a private survey, and they have not much to gain by one answer or another. Why then would there be any systemic bias? Maybe people rate games they are good at as being highly skill dependent, as a kind of ego stroking. But since people have many different favorite games, this should roughly average out across people. I discarded some bad data (games rated at or neat 0). I think these were mostly honest mistakes using the sliders. You can see the survey here. A few people (3) provided unserious data (very low ratings across the board), so I discarded them. Results for the remaining raters:
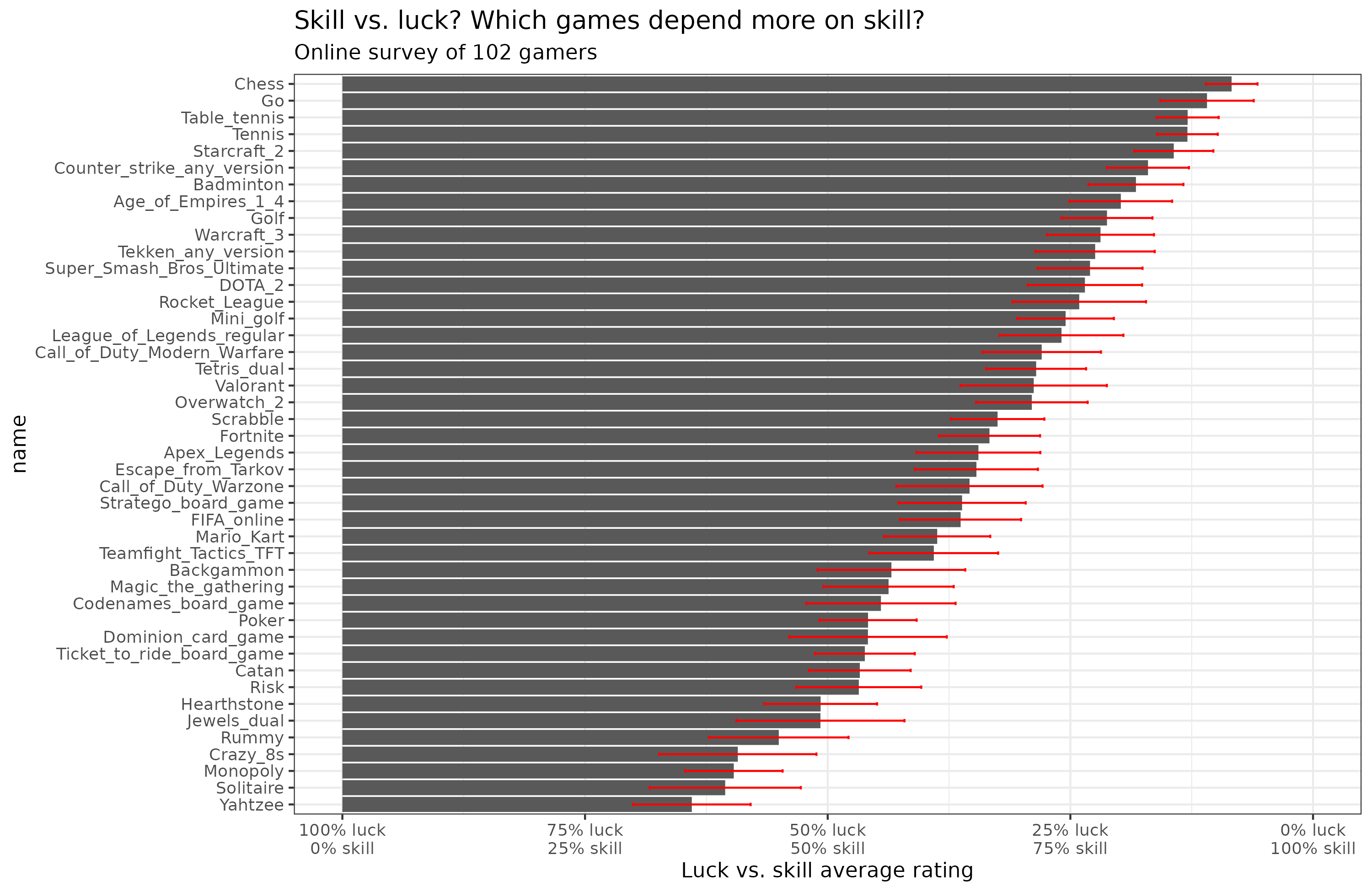
The error bars show the 95% confidence intervals. We see a wide distribution of skill vs. luck in the 44 games we included. In the top 4 games there is no or very little dice luck, but people still perceive some amount of luck, presumably related to the performance luck that we defined above (they are all perfect information games, or close to). Poker is perceived to be about half skill and luck, and popular family games like Monopoly are somewhat more about luck than skill. I think family games are generally designed to have a large luck component so that players of a wide range of skill level have a decent chance of winning. In a family setting, usually there is a wide range of skill levels, and grandma and little Peter age 9 should both have a decent chance of winning.
For good measure, let’s validate our survey method by their objective empirical results for the overlapping 11 games:
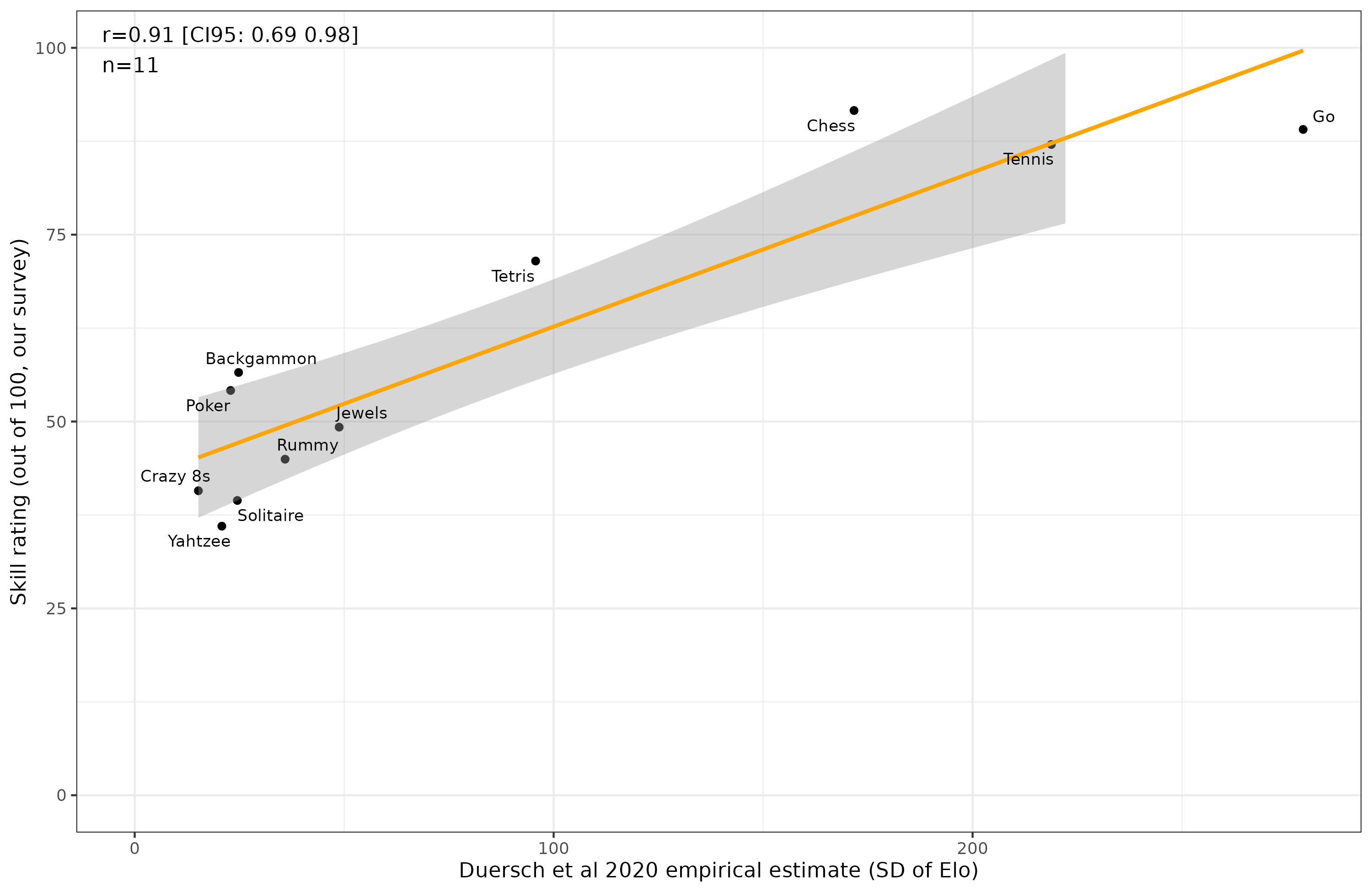
We obtain good concordance in terms of the relative differences (r = .91). There is some inconsistency in the scaling. Games with an Elo SD of near zero should show majority luck component in the ratings, but people seem to still estimate the skill component as being quite high. This could be interpreted as people overestimating their influence on the game.
Furthermore, we can check that our survey shows that the raters are somewhat in agreement. The intraclass correlation (ICC, random raters) is 38% (‘poor’), but the average ICC is 98%. Hence, the aggregate ratings are extremely reliable, but the individual ratings are only fairly reliable. The median correlation between one rater and other raters’ average is .81. The relatively low ICC at the individual level results from raters using somewhat different scales (e.g., one rater assigns Chess 80 and Poker 40, and another assigns them 100, and 60; relative difference may be about the same, but the absolute values are not). Visually:

So a few raters disagree with just about everybody else, but most people agree with each other very strongly, hence a median correlation of .81, but a mean of .71.
Conclusions
- It is possible to mathematically compare games for the relative importance of luck vs. skill. We have defined three kinds of luck in games, where games differ in the proportion of each of these.
- These values can be estimated by surveys of gamers with high relative accuracy (Pearson correlation). The survey finds that traditional ‘luck free’ board games like Chess and Go have very high skill ratings, real-time strategy games also very high. Various complex card or card-like games are intermediate.
- It would be ideal if the mathematical modeling of skill vs. luck in games could be extended to cover more of the games covered by the survey here, so that we can be more certain in the validity of survey (n = 11 overlapping games in this study).
- Of course, if you play any game long enough, your Elo (or MMR) will eventually reflect your true skill level, as the chance elements will average out. But performance in a given game can be highly variable depending on the game.