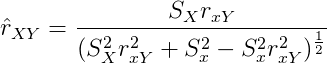Restriction of range is when the variance in some variable is reduced compared to the true population variance. This lowers the correlation between this variable and other variables. It is a common problem with research on students which are selected for general intelligence (GI) and hence have a lower variance. This means that correlations between GI and whatever found in student samples is too low.
There are some complicated ways to correct for restriction of range. The usual formula used is this:
which is also known as Thorndike’s case 2, or Pearson’s 1903 formula. Capital XY are the unrestricted variables, xy the restricted. The hat on r means estimated.
However, in a paper in review I used the much simpler formula, namely: corrected r = uncorrected r / (SD_restricted/SD_unrestricted) which seemed to give about the right results. But I wasn’t sure this was legit, so I did some simulations.
First, I selected a large range of true population correlations (.1 to .8) and a large range of selectivity (.1 to .9), then I generated very large datasets with each population correlation. Then for each restriction, I cut off the datapoints where the one variable was below the cutoff point, and calculated the correlation in that restricted dataset. Then I calculated the corrected correlation. Then I saved both pieces of information.
This gives us these correlations in the restricted samples (N=1,000,000)
| cor/restriction | R 0.1 | R 0.2 | R 0.3 | R 0.4 | R 0.5 | R 0.6 | R 0.7 | R 0.8 | R 0.9 |
| r 0.1 | 0.09 | 0.08 | 0.07 | 0.07 | 0.06 | 0.06 | 0.05 | 0.05 | 0.04 |
| r 0.2 | 0.17 | 0.15 | 0.14 | 0.13 | 0.12 | 0.11 | 0.10 | 0.09 | 0.08 |
| r 0.3 | 0.26 | 0.23 | 0.22 | 0.20 | 0.19 | 0.17 | 0.16 | 0.14 | 0.12 |
| r 0.4 | 0.35 | 0.32 | 0.29 | 0.27 | 0.26 | 0.24 | 0.22 | 0.20 | 0.17 |
| r 0.5 | 0.44 | 0.40 | 0.37 | 0.35 | 0.33 | 0.31 | 0.28 | 0.26 | 0.23 |
| r 0.6 | 0.53 | 0.50 | 0.47 | 0.44 | 0.41 | 0.38 | 0.36 | 0.33 | 0.29 |
| r 0.7 | 0.64 | 0.60 | 0.57 | 0.54 | 0.51 | 0.48 | 0.45 | 0.42 | 0.37 |
| r 0.8 | 0.75 | 0.71 | 0.68 | 0.65 | 0.63 | 0.60 | 0.56 | 0.53 | 0.48 |
The true population correlation is in the left-margin. The amount of restriction in the columns. So we see the effect of restricting the range.
Now, here’s the corrected correlations by my method:
| cor/restriction | R 0.1 | R 0.2 | R 0.3 | R 0.4 | R 0.5 | R 0.6 | R 0.7 | R 0.8 | R 0.9 |
| r 0.1 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.09 |
| r 0.2 | 0.20 | 0.20 | 0.20 | 0.20 | 0.21 | 0.21 | 0.20 | 0.20 | 0.20 |
| r 0.3 | 0.30 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.30 | 0.30 | 0.29 |
| r 0.4 | 0.41 | 0.41 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 |
| r 0.5 | 0.52 | 0.53 | 0.53 | 0.54 | 0.54 | 0.55 | 0.55 | 0.56 | 0.56 |
| r 0.6 | 0.63 | 0.65 | 0.66 | 0.67 | 0.68 | 0.69 | 0.70 | 0.70 | 0.72 |
| r 0.7 | 0.76 | 0.79 | 0.81 | 0.83 | 0.84 | 0.86 | 0.87 | 0.89 | 0.90 |
| r 0.8 | 0.89 | 0.93 | 0.97 | 1.01 | 1.04 | 1.07 | 1.10 | 1.13 | 1.17 |
Now, the first 3 rows are fairly close deviating by max .1, but it the rest deviates progressively more. The discrepancies are these:
| cor/restriction | R 0.1 | R 0.2 | R 0.3 | R 0.4 | R 0.5 | R 0.6 | R 0.7 | R 0.8 | R 0.9 |
| r 0.1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.01 |
| r 0.2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 |
| r 0.3 | 0.00 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | -0.01 |
| r 0.4 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| r 0.5 | 0.02 | 0.03 | 0.03 | 0.04 | 0.04 | 0.05 | 0.05 | 0.06 | 0.06 |
| r 0.6 | 0.03 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.10 | 0.10 | 0.12 |
| r 0.7 | 0.06 | 0.09 | 0.11 | 0.13 | 0.14 | 0.16 | 0.17 | 0.19 | 0.20 |
| r 0.8 | 0.09 | 0.13 | 0.17 | 0.21 | 0.24 | 0.27 | 0.30 | 0.33 | 0.37 |
So, if we can figure out how to predict the values in these cells from the two values in the row and column, one can make a simpler way to correct for restriction.
Or, we can just use the correct formula, and then we get:
| cor/restriction | R 0.1 | R 0.2 | R 0.3 | R 0.4 | R 0.5 | R 0.6 | R 0.7 | R 0.8 | R 0.9 |
| r 0.1 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.09 |
| r 0.2 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.21 | 0.20 |
| r 0.3 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 |
| r 0.4 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.39 | 0.39 |
| r 0.5 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.49 |
| r 0.6 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 |
| r 0.7 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.71 |
| r 0.8 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 |
With discrepancies:
| cor/restriction | R 0.1 | R 0.2 | R 0.3 | R 0.4 | R 0.5 | R 0.6 | R 0.7 | R 0.8 | R 0.9 |
| r 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.01 |
| r 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.01 | 0 |
| r 0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| r 0.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.01 | -0.01 |
| r 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.01 |
| r 0.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| r 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.01 |
| r 0.8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Pretty good!
Also, I need to re-do my paper.
R code:
library(MASS)
library(Hmisc)
library(psych)
pop.cors = seq(.1,.8,.1) #population correlations to test
restrictions = seq(.1,.9,.1) #restriction of ranges in centiles
sample = 1000000 #sample size
#empty dataframe for results
results = data.frame(matrix(nrow=length(pop.cors),ncol=length(restrictions)))
colnames(results) = paste("R",restrictions)
rownames(results) = paste("r",pop.cors)
results.c = results
results.c2 = results
#and fetch!
for (pop.cor in pop.cors){ #loop over population cors
data = mvrnorm(sample, mu = c(0,0), Sigma = matrix(c(1,pop.cor,pop.cor,1), ncol = 2),
empirical = TRUE) #generate data
rowname = paste("r",pop.cor) #get current row names
for (restriction in restrictions){ #loop over restrictions
colname = paste("R",restriction) #get current col names
z.cutoff = qnorm(restriction) #find cut-off
rows.to.keep = data[,1] > z.cutoff #which rows to keep
rdata = data[rows.to.keep,] #cut away data
cor = rcorr(rdata)$r[1,2] #get cor
results[rowname,colname] = cor #add cor to results
sd = describe(rdata)$sd[1] #find restricted sd
cor.c = cor/sd #corrected cor, simple formula
results.c[rowname,colname] = cor.c #add cor to results
cor.c2 = cor/sqrt(cor^2+sd^2-sd^2*cor^2) #correct formula
results.c2[rowname,colname] = cor.c2 #add cor to results
}
}
#how much are they off by?
discre = results.c
for (num in 1:length(pop.cors)){
cor = pop.cors[num]
discre[num,] = discre[num,]-cor
}
discre2 = results.c2
for (num in 1:length(pop.cors)){
cor = pop.cors[num]
discre2[num,] = discre2[num,]-cor
}