Blog

This is a nerdy post of little interest to the layman.

There’s this old paper that sometimes comes up:

• Dana, J., & Dawes, R. M. (2004). The superiority of simple alternatives to regression for social science predictions. Journal of Educational and Behavioral Statistics, 29(3), 317-331.

Some simple, nonoptimized coefficients (e.g., correlation weights, equal weights) were pitted against regression in extensive prediction competitions. After drawing calibration samples from large supersets of real and synthetic data, the researchers observed which set of sample-derived coefficients made the best predictions when applied back to the superset. When adjusted R from the calibration sample was < .6, correlation weights were typically superior to regression coefficients, even if the sample contained 100 observations per predictor; unit weights were likewise superior to all methods if adjusted R was < .4. Correlation weights were generally the best method. It was concluded that regression is rarely useful for prediction in most social science contexts.

Their main figure is this one:

It’s not that easy to interpret by looking at it. What they did was simulate several rounds of data with different true betas for variables in a dataset. The size of the dataset and the number of predictors was varied. “m” is the number of predictors, so that e.g. 10m means the sample size was 10 * m. They used 4 different models to predict new unseen data, so that test results could be interpreted free of overfitting bias. In general, when the best possible validity was relatively modest, say, R = 0.30 (r² = 10%), unit weights worked well, better than trying to estimate optimal weights. As the best possible prediction increased, unit weights became increasingly worse. Depending on what kind of data situation one is in, this may mean that unit weights are a better and simpler option. To test this one real world datasets, they gathered a few datasets and used subsetting to avoid overfitting. The outcome was one continuous variable and the others served as the predictors.

For instance:

The WLS dataset includes a subset of results from the Wisconsin Longitudinal Survey (1993). The criterion was a measure of occupational prestige in 1992. Predictors were self-rated physical health compared to others of same age and gender (healthier), scores on personality scales measuring depression (less depressed), extraversion (more extraverted), neuroticism (less neurotic), and number of children.

In this case, since the best prediction that could be made was modest (best R = 0.20), trying to estimate optimal weights was actually worse than using unit weights, even when the sample size was 50 cases per variable. In the Abalone dataset, prediction was easy (best R = 0.71) and here unit weights was not as impressive. However, in relative terms, it performed well: 0.57 vs. 0.71 at max sample size (80% of optimal).

I decided to redo some of the simulations. The first task was to simulate realistic correlation matrices. This proved difficult since correlation matrices must conform to certain mathematical rules (positive definiteness). To give an obvious example of something impossible. If there are 3 variables, [A, B, C], it is not possible for r(A,B) = 1, and r(A,C) = 1 while r(B,C) < 1. Correlations are semi-transitive. So one can’t just pick random values from a uniform distribution [-1,1], populate the matrix and call it a day. Instead, I looked around for someone who solved the problem already and found a few. In the end, I ended up implement my own solution based on PCA because theirs did not easily allow one to verify the strength of the correlations. Mine is still not quite right and it’s much slower since it involves generating case data to ensure the matrices are valid.

Armed with the ability to generate random correlation matrices, I had the ability to generate random data and true models. The true model being the set of true weights sampled from some distribution (normal) that when multiplied with each of the variables results in the outcome variable (Y), plus some noise to control the level of predictiveness (it would be R = 1.0 with no noise). So I simulated 114k datasets with these parameter variations:

• n = seq(50, 500, by = 25)
  • Sample size of training set, test set was always 500.
• preds = c(5, 10, 15, 20, 25)
  • Number of predictors, all which have a random normal true beta
• y_noise = c(0.5, 1, 1.5, 2, 3, 4)
  • The amount of noise (random error) to add the true standardized y variable to lower the maximum validity a model can achieve.
• x_noise = c(0.5, 1, 2, 3)
  • The amount of noise to add the to predictors to lower their intercorrelations.
• reps = 1:50
  • Number of repeats for each set of parameters above to reduce sampling error.

The overall results are these:

Across the parameters, sample size has a major effect on the model validity (recall, this is on the test set), not so surprising. The methods were:

• OLS: standard regression
• ridge regression: same as above but with a penalty parameter to reduce overfitting
• correlation weights: use the correlations between each predictor and the outcome as its regression weights
• cor unit weights: use correlation sign to determine whether the beta weight is 1 or -1, unit weights
• reg unit weights: use OLS betas to determine the sign for unit weights

The results show that the best method in general in ridge regression. The simpler methods did not beat OLS at any sample size, which is in contrast with Dana and Dawes’ results. But maybe we need to look only at the hard cases, with low validity of the model (y_noise = 4), lots of predictors (preds = 25), and strong correlations between predictors (x_noise = 0.5). With these:

Ridge regression still wins at all sample sizes, but notice how bad OLS is here. It’s not so surprising if you think about it. OLS is given 25 correlated predictors. It achieves barely above chance, whereas the maximum is more than 0.20. Using the betas from OLS to set unit weights performed even worse. However, the correlation weights approaches were pretty solid. OLS does not beat them even at n=500.

Digging further into this, we can isolate the effect of noise in the outcome by looking at simulations with n=50, preds=25, x_noise=0.5:

In this very tough situation, OLS only wins when the outcome is extremely predictable (y_noise = 0.5), unrealistically so for real data.

How does predictor intercorrelations affect things? We can isolate this by filtering results to n=50, preds=25, y_noise=2. Results are too boring to look at but they show OLS does very poorly, being the second worst method. Correlation weights is still 2nd best.

What about number of predictors? Filtering to n = 50, y_noise = 2:

OLS does very poorly as the number of predictors increases towards 25 (case to predictor ratio of only 2), but it does fine when there’s more realistic smaller numbers.

Overall, I found that:

• Per Dana & Dawes, I replicate the advantages of correlation weights, and in some extreme situations, unit weights from correlations.
• Ridge regression beats the other methods in every situation, but correlation weights is usually close.
• OLS does quite poorly when there are too many predictors for the sample size, or the outcome is hard to predict.

Applications?

There are some applications of these kinds of findings. For instance, when you can assume all predictors have positive betas (or factor loadings), then unit weights will work almost as well as weighted scores. This is why so-called unit weighted factor analysis (average of z-scored variables) works well. This is fortunate because most scoring of scales in social science uses unit weights (each item on e.g. extroversion scale counts the same).

Even in genomics, there are some applications. GWASs only estimate the (standalone) beta of each variant (snp) with limited accuracy, so one might be inclined to just consider all the positive betas as 1, and negative betas as -1 for the purpose of scoring. Does this work? Yes:

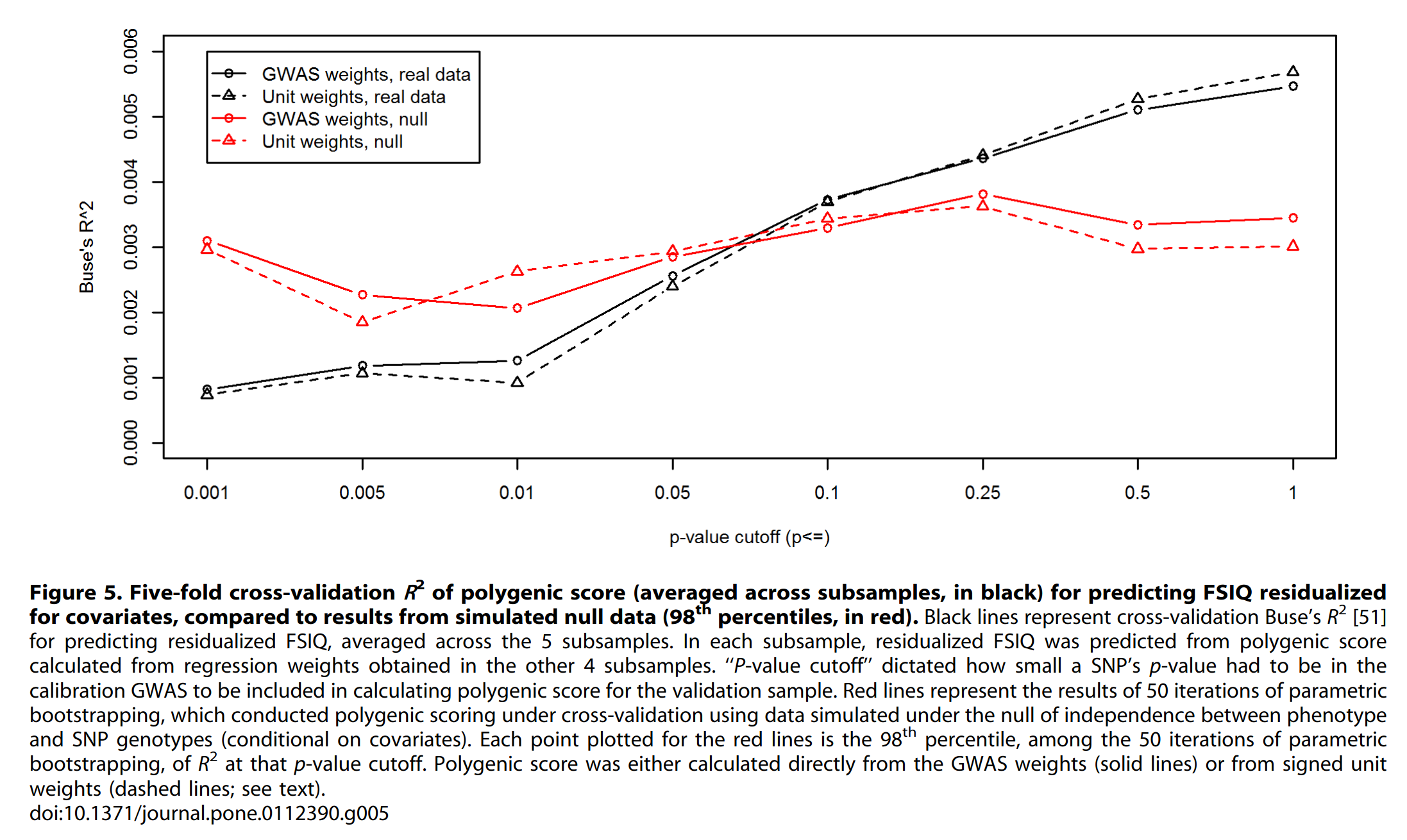
The major caveat here is that this is from 2014 using EA1, that’s why the polygenic score validity is terrible. David Reich’s team that did the study on “West Eurasian” ancient genomes recently also used unit weights as a robustness check, with similar findings. The genomics equivalent of the correlation weights approach is the weighted polygenic score without clumping. Normally, variants close on the genome are correlated, so counting all of them would lead to some double counting of the same signal of the unobserved assumed causal variant(s). For this reason, usually one variant is picked as the best guess causal variant based on biological annotations (e.g. non-synonymous) or with the strongest evidence of signal (lowest p value). The simulation results here suggest maybe clumping isn’t so important, at least for comparing subjects within the same ethnic group.