Blog

You are currently viewing Heritabilities are usually underestimated

Heritabilities are usually underestimated

When we read popular books by leading authors, we often find statements like this:

Since the 1960s scientists conducting long-term studies on special relatives like twins and adoptees have built a mountain of evidence showing that genetics contributes importantly to psychological differences between us. The genetic contribution is not just statistically significant, it is massive. Genetics is the most important factor shaping who we are. It explains more of the psychological differences between us than everything else put together. For example, the most important environmental factors, such as our families and schools, account for less than 5 per cent of the differences between us in our mental health or how well we did at school – once we control for the impact of genetics. Genetics accounts for 50 per cent of psychological differences, not just for mental health and school achievement, but for all psychological traits, from personality to mental abilities. I am not aware of a single psychological trait that shows no genetic influence.

This is from Robert Plomin’s Blueprint. In fact, Plomin repeats this 50% value something like 20 times. So it must be quite a well established value, right? It is in fact a rather large underestimate. Why? We can go into the various assumptions of typical family studies, but the short story is that these are some known biases:

  1. Assortative mating for a trait results in heritabilities being underestimated when using the MZ-DZ method (classical twin design).
  2. Measurement error for a trait results in heritabilities being underestimated pretty much no matter which design is used.
  3. Violations of the equal environment assumption (EEA) may result in heritability being overestimated.
  4. Heritability increases with age (Wilson effect). Thus if one wants an artificial low (unrepresentative) value, use data from young children. Famously done by Devlin 1997, and Richard Nisbett loves this tactic. This is not really a method bias as such, but a sampling bias when aggregating data.

As you can imagine with socialist science, almost all focus has been on trying in vain to prove (3) or defend it against attacks. This debate has essentially been concluded as even the leftists have given up attacking it with some stragglers like Jay Joseph left. A useful review is Felson 2014, who leaned back hard to try to make something out of it but really couldn’t get much. I recommend the reviews by Wright et al 2014, and Wright et al 2015.

So OK, (3) isn’t a big deal, but may have some marginal effect. What about the other two, how do researchers deal with them? Short answer: they don’t. They almost completely ignore them. Arthur Jensen deserves credit for clearly spelling out very early on why this is a mistake. In his 1969 review How much can we boost IQ and scholastic achievement? (see the review of the review):

The situation is relatively simple when we deal only with MZ twins, who are genetically identical, or with unrelated children, who have nothing in common genetically. But in order to estimate heritability from any of the other kinship correlations, much more complex formulas are needed which would require much more explanation than is possible in this article. I have presented elsewhere a generalized formula for estimating heritability from any two kinship correlations where one kinship is of a high er degree than the other (Jensen, 1967a). I applied this heritability formula to all the correlations for monozygotic and dizygotic (half their genes in common) twins reported in the literature and found an average heritability of .80 for intelligence test scores. (The correlations from which this heritability estimate was derived were corrected for unreliability.) Environmental differences between families account for .12 of the total variance, and differences within families account for .08. It is possible to derive an overall heritability coefficient from all the kinship correlations given in Table 2. This composite value of H is .77, which becomes .81 after correction for unreliabil­ity (assuming an average test reliability of .95). Th is represents probably the best single overall estimate of the heritability of measured intelligence that we can make. But, as pointed out previously, this is an average value of H about which there is some dispersion of values, depending on such variables as the particular tests used, the population sampled, and sampling error.

In the same article he also deals with assortative mating. Correcting for this means one has to upwardly adjust the estimates a bit. If you read random papers using twin designs, they rarely mention these problems. I speculate that they don’t want to attract too much negative attention for their findings. It is hard enough to get people to accept 50% heritability, and <10% shared environment, but if you also want to tell people, that — akshually — the real values are more like 70-80% and <5%, you may get even more raised eyebrows.

OK, cheap enough talk, so let’s look at some examples.

Personality

First, personality. In my 2017 review post on measurement in personality, I summarized some of these studies. Repeat here for convenience:

Measured personality constructs via self- and peer reports on the items of the NEO Five-Factor Inventory. The sample included 660 monozygotic and 200 same sex and 104 opposite sex dizygotic twin pairs. Participants were aged 14–80 yrs. Self- and 2 independent peer reports for each of the twins were collected. Analysis of self-report data replicates earlier findings of a substantial genetic influence on the Big Five. This influence was also found for peer reports. Results validate findings based solely on self-reports. However, estimates of genetic contributions to phenotypic variance were substantially higher when based on peer reports or self- and peer reports because these data allowed for the separation of error variance from variance due to nonshared environmental influences. Correlations between self- and peer reports reflected the same genetic influences to a much higher extent than identical environmental effects.

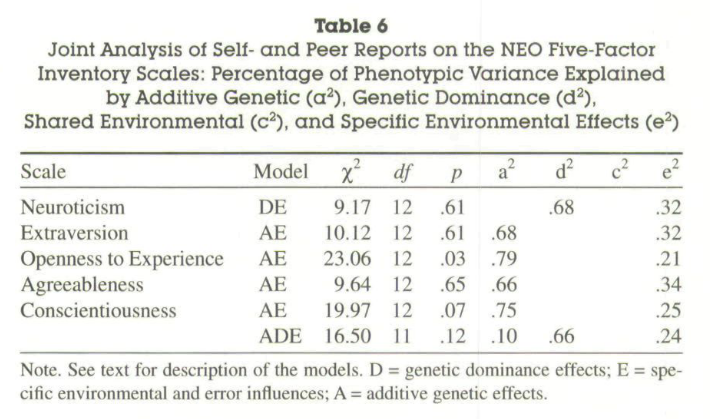
OCEAN (big five) personality values are now from 66% to 79%. The self-report based values were at 42-56%. The peer-report  based values were 57-81%. Clearly, better measurement results in higher heritability estimates. It also underscores that there are two classes of measurement errors. First, random measurement error, which is what it sounds like, random noise. This just reduces the effect sizes towards 0, and in family studies, inflates the ‘unshared environment’ leftover component. Second, systemic measurement errors, which is when we aren’t measuring exactly the construct we want, but also something else, such as self-evaluation bias. The strength of studies like this one is that they combine self- and peer-reports to average out some of this bias.

We describe a behavioural genetic extension of the classic multitrait‐multimethod study design that allows estimating genetic and environmental influences on method effects in twin studies (MTMM‐T). Genetic effects and effects of the environment shared by siblings are interpreted as indicators of convergent validity. In an application of the MTMM study design, we used self‐ and peer report data to examine the higher‐order structure of the NEO‐PI‐R. Structural equation modelling did not support a general factor of personality in multimethod data. The higher‐order factor Stability turns out to be, at most, a weak trait factor. Genetic effects on method factors indicate that especially self‐reports but also peer reports show convergent validity between twins but not between methods.

In this follow-up study by the same authors, we get more of the same. This time they used better methods to analyze the specific systemic measurement bias components.

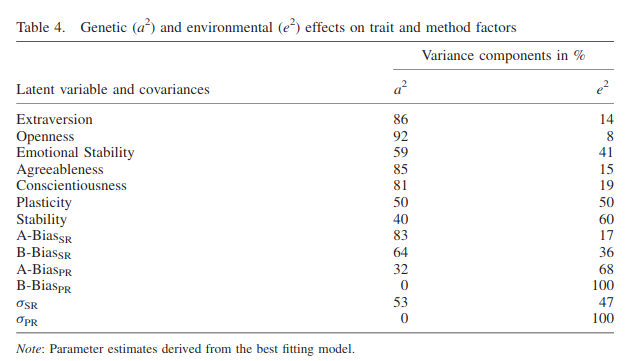
Taking these into account, they report heritabilities for OCEAN of 59-92%.

Self-control is the ability to control one’s impulses when faced with challenges or temptations, and is robustly associated with physiological and psychological well-being. Twin studies show that self-control is heritable, but estimates range between 0% and 90%, making it difficult to draw firm conclusions. The aim of this study was to perform a meta-analysis to provide a quantitative overview of the heritability of self-control. A systematic search resulted in 31 included studies, 17 reporting on individual samples, based on a sample size of >30,000 twins, published between 1997 and 2018. Our results revealed an overall monozygotic twin correlation of 0.58, and an overall dizygotic twin correlation of 0.28, resulting in a heritability estimate of 60%. The heritability of self-control did not vary across gender or age. The heritability did differ across informants, with stronger heritability estimates based on parent report versus self-report or observations. This finding provides evidence that when aiming to understand individual differences in self-control, one should take genetic factors into account. Recommendations for future research are discussed.

Again, higher heritability for better measurement, especially with other-reports.

Psychiatry

Background: In epidemiologie samples, the assessment of lifetime history (LTH) of major depression (MD) is not highly reliable. In female twins, we previously found that LTH of MD, as assessed at a single personal interview, was moderately heritable (approximately 40%). In that analysis, errors of measurement could not be discriminated from true environmental effects.

Methods: In 1721 female twins from a population based register, including both members of 742 pairs, LTH of MD, covering approximately the same time period, was obtained twice, once by self-administered questionnaire and once at personal interview.

Results: Reliability of LTH of MD was modest (×= + .34, tetrachoric r= + .56) and was predicted by the number of depressive symptoms, treatment seeking, number of episodes, and degree of impairment. Deriving an “index of caseness” from these predictors, the estimated heritability of LTH of MD was greater for more restrictive definitions. Incorporating error of measurement into a structural equation model including both occasions of measurement, the estimated heritability of the liability to LTH of MD increased substantially (approximately 70%). More than half of what was considered environmental effects when LTH of MD was analyzed on the basis of one assessment appeared, when two assessments were used, to reflect measurement error.

Conclusions: Major depression, as assessed over the lifetime, may be a rather highly heritable disorder of moderate reliability rather than a moderately heritable disorder of high reliability.

Abstract says it all.

Decades of research show that genes play an vital role in the etiology of attention deficit hyperactivity disorder (ADHD) and its comorbidity with other disorders. Family, twin, and adoption studies show that ADHD runs in families. ADHD’s high heritability of 74% motivated the search for ADHD susceptibility genes. Genetic linkage studies show that the effects of DNA risk variants on ADHD must, individually, be very small. Genome-wide association studies (GWAS) have implicated several genetic loci at the genome-wide level of statistical significance. These studies also show that about a third of ADHD’s heritability is due to a polygenic component comprising many common variants each having small effects. From studies of copy number variants we have also learned that the rare insertions or deletions account for part of ADHD’s heritability. These findings have implicated new biological pathways that may eventually have implications for treatment development.

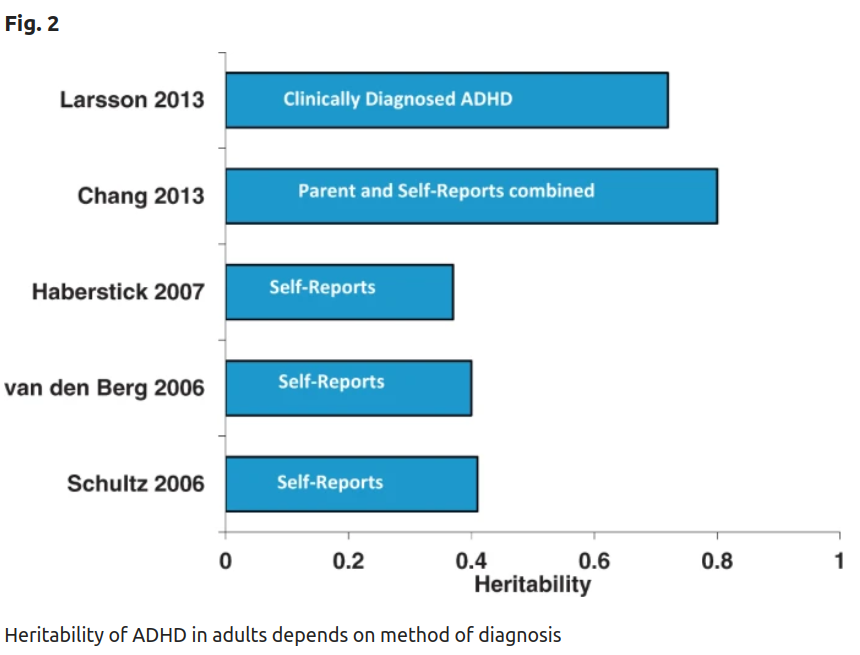
Self-report ADHD heritability about 40%, clinical diagnosis, ~70%, combined measurements, ~80%. This ~70% from diagnosis is on the low side, consider this 2017 massive Swedish population data study:

The concordance rates and tetrachoric correlations in the different groups of siblings are shown in Table 3. The sex and birth year-adjusted tetrachoric correlation of ADHD was 0.90 (95% CI = 0.83–0.95) for MZ twins, 0.51 (95% CI = 0.43–0.59) for DZ twins, 0.44 (95% CI = 0.43–0.45) for full siblings, 0.24 (95% CI = 0.20–0.28) for maternal half-siblings, and 0.18 (95% CI = 0.13–0.23) for paternal half- siblings. In the ADCE model, the variance of the liability of ADHD attributable to additive genetic effects was estimated to be 0.69 (95% CI = 0.50–0.88); dominant genetic effects, 0.14 (95% CI = 0.00–0.30); shared environment, 0.06 (95% CI = 0.00–0.13); nonshared environment, 0.10 (95% CI = 0.06–0.16). The likeli- hood ratio tests showed that the ACE model (dropping only D parameter) did not result in a significant loss in fit, whereas the ADE model (dropping only C param- eter) did (Table 4). The AE model (dropping both D and C parameters) was selected as the best fitting model, where the heritability of ADHD was estimated to be 0.89 (95% CI = 0.87–0.91).

Physical traits

Physical traits usually have better measurement, as we have nice ratio scales (kilograms). Still, there is some error in measurement, especially if we rely on self-report or self-measurement:

Evidence for a major role of genetic factors in the determination of body mass index (BMI) comes from studies of related individuals. Despite consistent evidence for a heritable component of BMI, estimates of BMI heritability vary widely between studies and the reasons for this remain unclear. While some variation is natural due to differences between populations and settings, study design factors may also explain some of the heterogeneity. We performed a systematic review that identified 88 independent estimates of BMI heritability from twin studies (total 140,525 twins) and 27 estimates from family studies (42,968 family members). BMI heritability estimates from twin studies ranged from 0.47 to 0.90 (5th/50th/95th centiles: 0.58/0.75/0.87) and were generally higher than those from family studies (range: 0.24–0.81; 5th/50th/95th centiles: 0.25/0.46/0.68). Meta-regression of the results from twin studies showed that BMI heritability estimates were 0.07 (P = 0.001) higher in children than in adults; estimates increased with mean age among childhood studies (+0.012/year, P = 0.002), but decreased with mean age in adult studies (−0.002/year, P = 0.002). Heritability estimates derived from AE twin models (which assume no contribution of shared environment) were 0.12 higher than those from ACE models (P < 0.001), whilst lower estimates were associated with self reported versus DNA-based determination of zygosity (−0.04, P = 0.02), and with self reported versus measured BMI (−0.05, P = 0.03). Although the observed differences in heritability according to aspects of study design are relatively small, together, the above factors explained 47% of the heterogeneity in estimates of BMI heritability from twin studies. In summary, while some variation in BMI heritability is expected due to population-level differences, study design factors explained nearly half the heterogeneity reported in twin studies. The genetic contribution to BMI appears to vary with age and may have a greater influence during childhood than adult life.

The p values aren’t impressive, but they suggest about 4% underestimate from not classifying twins correctly (people don’t always know if they are identical or dizygotic twins!) and another 5% depending on whether the measurements of height and weight were done by a professional or by people themselves.

Intelligence / cognition

First, consider a study that takes assortative mating into account. This can be done using extended family designs, see my review of all such studies here (almost none of which find sizable effects of parenting per se):

  • Vinkhuyzen, A. A., Van Der Sluis, S., Maes, H. H., & Posthuma, D. (2012). Reconsidering the heritability of intelligence in adulthood: taking assortative mating and cultural transmission into account. Behavior genetics, 42(2), 187-198.

Heritability estimates of general intelligence in adulthood generally range from 75 to 85%, with all heritability due to additive genetic influences, while genetic dominance and shared environmental factors are absent, or too small to be detected. These estimates are derived from studies based on the classical twin design and are based on the assumption of random mating. Yet, considerable positive assortative mating has been reported for general intelligence. Unmodeled assortative mating may lead to biased estimates of the relative magnitude of genetic and environmental factors. To investigate the effects of assortative mating on the estimates of the variance components of intelligence, we employed an extended twin-family design. Psychometric IQ data were available for adult monozygotic and dizygotic twins, their siblings, the partners of the twins and siblings, and either the parents or the adult offspring of the twins and siblings (N = 1314). Two underlying processes of assortment were considered: phenotypic assortment and social homogamy. The phenotypic assortment model was slightly preferred over the social homogamy model, suggesting that assortment for intelligence is mostly due to a selection of mates on similarity in intelligence. Under the preferred phenotypic assortment model, the variance of intelligence in adulthood was not only due to non-shared environmental (18%) and additive genetic factors (44%) but also to non-additive genetic factors (27%) and phenotypic assortment (11%). This non-additive nature of genetic influences on intelligence needs to be accommodated in future GWAS studies for intelligence.

I can’t really tell what their phenotypic assortment is supposed to mean, I assume it is their assortative mating genetic component, so we add all of these and get 82%. This study does not appear to have adjusted for random measurement error, but it does take assortative mating into account. For random measurement error, we can either post-hoc adjust the correlations/covariances, or we can use a full SEM approach. The latter is preferable. I know of two studies that did this:

Despite an extensive literature, the “g” construct remains a point of debate. Different models explaining the observed relationships among cognitive tests make distinct assumptions about the role of g in relation to individual tests and specific cognitive domains. Surprisingly, these different models and their corresponding assumptions are rarely tested against one another. In addition to the comparison of distinct models, a multivariate application of the twin design offers a unique opportunity to test whether there is support for g as a latent construct with its own genetic and environmental influences, or whether the relationships among cognitive tests are instead driven by independent genetic and environmental factors. Here we tested multiple distinct models of the relationships among cognitive tests utilizing data from the Vietnam Era Twin Study of Aging (VETSA), a study of middle-aged male twins. Results indicated that a hierarchical (higher-order) model with a latent g phenotype, as well as specific cognitive domains, was best supported by the data. The latent g factor was highly heritable (86%), and accounted for most, but not all, of the genetic effects in specific cognitive domains and elementary cognitive tests. By directly testing multiple competing models of the relationships among cognitive tests in a genetically-informative design, we are able to provide stronger support than in prior studies for g being a valid latent construct.

The main beef with this study is that the sample is somewhat small for a twin study:

The present analyses were based on data from 346 monozygotic (MZ) twin pairs, 265 dizygotic (DZ) twin pairs, and 12 unpaired twins for whom valid cognitive assessment data were obtained. The average age was 55.4 years (SD = 2.5), and the average years of education was 13.8 (SD = 2.1, Range = 8 to 20).

These are of course very good for the standards of social science.

  • Shikishima, C., Hiraishi, K., Yamagata, S., Sugimoto, Y., Takemura, R., Ozaki, K., … & Ando, J. (2009). Is g an entity? A Japanese twin study using syllogisms and intelligence tests. Intelligence, 37(3), 256-267.

Using a behavioral genetic approach, we examined the validity of the hypothesis concerning the singularity of human general intelligence, the g theory, by analyzing data from two tests: the first consisted of 100 syllogism problems and the second a full-scale intelligence test. The participants were 448 Japanese young adult twins (167 pairs of identical and 53 pairs of fraternal twins). Data were analyzed for their fit to two kinds of multivariate genetic models: a common pathway model, in which a higher-order latent variable, g, was postulated as an entity; and an independent pathway model, in which the higher-order latent variable was not posited. These analyses revealed that the common pathway model which included additive genetic and nonshared environmental factors best accounted for the three distinct mental abilities: syllogistic logical deductive reasoning, verbal, and spatial. Both the substantial g-loading for syllogism-solving, historically recognized as the symbol of human intelligence, and the emergence of g as an entity at an etiological level, that is, at the genetic and environmental factor level, provide further support for the g theory.

The common latent construct was revealed to be highly heritable, with a heritability of 83% (95% CI: 74–88%). [from paper]

An even smaller study, but same approach.

  • Harden, K. P., Engelhardt, L. E., Mann, F. D., Patterson, M. W., Grotzinger, A. D., Savicki, S. L., … & Tucker-Drob, E. M. (2020). Genetic associations between executive functions and a general factor of psychopathology. Journal of the American Academy of Child & Adolescent Psychiatry, 59(6), 749-758.

Objective Symptoms of psychopathology covary across diagnostic boundaries, and a family history of elevated symptoms for a single psychiatric disorder places an individual at heightened risk for a broad range of other psychiatric disorders. Both twin-based and genome-wide molecular methods indicate a strong genetic basis for the familial aggregation of psychiatric disease. This has led researchers to prioritize the search for highly heritable childhood risk factors for transdiagnostic psychopathology. Cognitive abilities that involve the selective control and regulation of attention, known as executive functions (EFs), are a promising set of risk factors.
Method In a population-based sample of child and adolescent twins (n = 1,913, mean age = 13.1 years), we examined genetic overlap between both EFs and general intelligence (g) and a transdiagnostic dimension of vulnerability to psychopathology, comprising symptoms of anxiety, depression, neuroticism, aggression, conduct disorder, oppositional defiant disorder, hyperactivity, and inattention. Psychopathology symptoms in children were rated by children and their parents.
Results Latent factors representing general EF and g were highly heritable (h2 = 86%−92%), and genetic influences on both sets of cognitive abilities were robustly correlated with transdiagnostic genetic influences on psychopathology symptoms (genetic r values ranged from −0.20 to −0.38).
Conclusion General EF and g robustly index genetic risk for transdiagnostic symptoms of psychopathology in childhood. Delineating the developmental and neurobiological mechanisms underlying observed associations between cognitive abilities and psychopathology remains a priority for ongoing research.

(Yes, that’s the same Paige Harden we know and love.) This same study also reported that parent-rated p factor had a heritability of 72% while self-report was only 49%.

The limitation of these studies is that they don’t report the heritabilities calculated from simpler modeling approach using sumscores, so we cannot directly show the contrast.

Criminal behavior

From the prior post on measuring criminal and antisocial behavior (I apparently wrote about this in 2016 too but forgot about it):

Genetic and environmental influences on childhood antisocial and aggressive behavior (ASB) during childhood were examined in 9- to 10-year-old twins, using a multi-informant approach. The sample (605 families of twins or triplets) was socioeconomically and ethnically diverse, representative of the culturally diverse urban population in Southern California. Measures of ASB included symptom counts for conduct disorder, ratings of aggression, delinquency, and psychopathic traits obtained through child self-reports, teacher, and caregiver ratings. Multivariate analysis revealed a common ASB factor across informants that was strongly heritable (heritability was .96), highlighting the importance of a broad, general measure obtained from multiple sources as a plausible construct for future investigations of specific genetic mechanisms in ASB. The best fitting multivariate model required informant-specific genetic, environmental, and rater effects for variation in observed ASB measures. The results suggest that parent, children, and teachers have only a partly “shared view” and that the additional factors that influence the “rater-specific” view of the child’s antisocial behavior vary for different informants. This is the first study to demonstrate strong heritable effects on ASB in ethnically and economically diverse samples.

Unfortunately, they also don’t report the ACE variance breakdowns for each of their methods, just the overall best fit.

  • Frisell, T., Pawitan, Y., Långström, N., & Lichtenstein, P. (2012). Heritability, assortative mating and gender differences in violent crime: results from a total population sample using twin, adoption, and sibling models. Behavior genetics, 42(1), 3-18.

Research addressing genetic and environmental determinants to antisocial behaviour suggests substantial variability across studies. Likewise, evidence for etiologic gender differences is mixed, and estimates might be biased due to assortative mating. We used longitudinal Swedish total population registers to estimate the heritability of objectively measured violent offending (convictions) in classic twin (N = 36,877 pairs), adoptee-parent (N = 5,068 pairs), adoptee-sibling (N = 10,610 pairs), and sibling designs (N = 1,521,066 pairs). Type and degree of assortative mating were calculated from comparisons between spouses of siblings and half-siblings, and across consecutive spouses. Heritability estimates for the liability of violent offending agreed with previously reported heritability for self-reported antisocial behaviour. While the sibling model yielded estimates similar to the twin model (A ≈ 55%, C ≈ 13%), adoptee-models appeared to underestimate familial effects (A ≈ 20-30%, C ≈ 0%). Assortative mating was moderate to strong (r (spouse) = 0.4), appeared to result from both phenotypic assortment and social homogamy, but had only minor effect on variance components. Finally, we found significant gender differences in the etiology of violent crime.

This study thus looked at controlling for assortative mating, finding it was very strong (r = 0.40!), but this didn’t affect the estimates so much. It seems that for crime, the more important problem is the measurement of the phenotype (in this study, convictions), not taking into account assortative mating.

We’ve seen again and again that heritabilities from most studies are routinely underestimated due to known biases from assortative mating (which is omnipresent for behavioral traits) and measurement errors: random and systemic. These sources of error are routinely ignored. Genetic influence on traits are pervasively underestimated, sometimes in the extreme, e.g. ADHD from 40% to 80%. So you should adjust upwards in your mind when reading findings.

Tags: , , ,