Since I keep having to look for these, here’s a compilation for ease of reference.
-
Hemphill, J. F. (2003). Interpreting the magnitudes of correlation coefficients. American Psychologist. Ungated
Discusses empirical guidelines for interpreting the magnitude of correlation coefficients, a key index of effect size, in psychological studies. The author uses the work of J. Cohen (see record 1987-98267-000), in which operational definitions were offered for interpreting correlation coefficients, and examines two meta-analytic reviews (G. J. Meyer et al., see record 2001-00159-003; and M. W. Lipsey et al., see record 1994-18340-001) to arrive at the empirical guidelines.
- Richard, F. D., Bond Jr, C. F., & Stokes-Zoota, J. J. (2003). One hundred years of social psychology quantitatively described. Review of General Psychology, 7(4), 331-363.
This article compiles results from a century of social psychological research, more than 25,000 studies of 8 million people. A large number of social psychological conclusions are listed alongside meta-analytic information about the magnitude and variability of the corresponding effects. References to 322 meta-analyses of social psychological phenomena are presented, as well as statistical effect-size summaries. Analyses reveal that social psychological effects typically yield a value of r equal to.21 and that, in the typical research literature, effects vary from study to study in ways that produce a standard deviation in r of.15. Uses, limitations, and implications of this large-scale compilation are noted.
-
Ellis, P. D. (2010). Effect sizes and the interpretation of research results in international business. Journal of International Business Studies, 41(9), 1581-1588.
Journal editors and academy presidents are increasingly calling on researchers to evaluate the substantive, as opposed to the statistical, significance of their results. To measure the extent to which these calls have been heeded, I aggregated the meta-analytically derived effect size estimates obtained from 965 individual samples. I then surveyed 204 studies published in the Journal of International Business Studies. I found that the average effect size in international business research is small, and that most published studies lack the statistical power to detect such effects reliably. I also found that many authors confuse statistical with substantive significance when interpreting their research results. These practices have likely led to unacceptably high Type II error rates and invalid inferences regarding real-world effects. By emphasizing p values over their effect size estimates, researchers are under-selling their results and settling for contributions that are less than what they really have to offer. In view of this, I offer four recommendations for improving research and reporting practices.
-
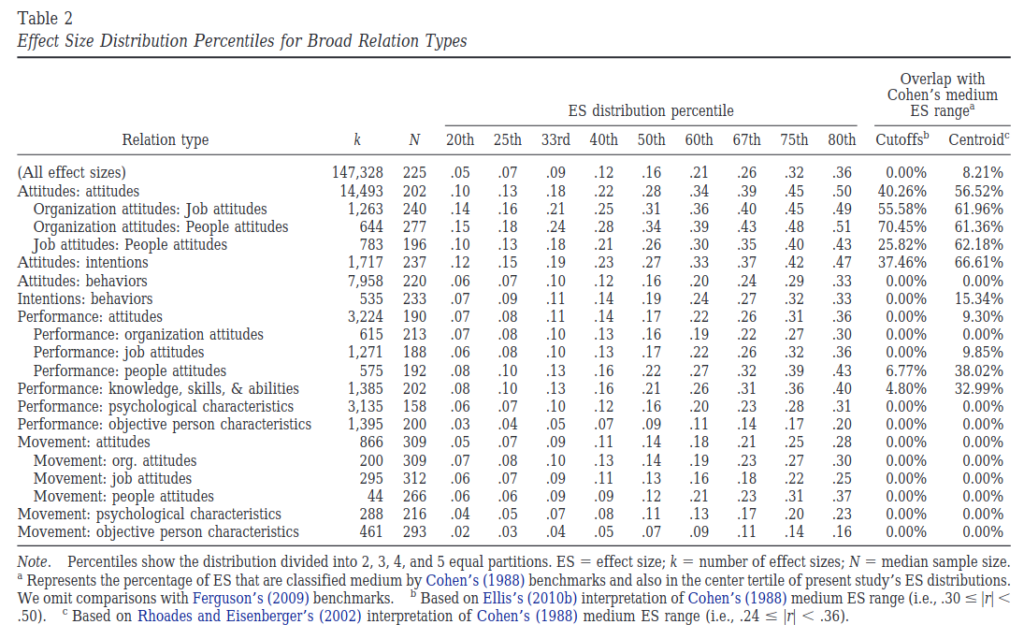
Bosco, F. A., Aguinis, H., Singh, K., Field, J. G., & Pierce, C. A. (2015). Correlational effect size benchmarks. Journal of Applied Psychology, 100(2), 431.
Effect size information is essential for the scientific enterprise and plays an increasingly central role in the scientific process. We extracted 147,328 correlations and developed a hierarchical taxonomy of variables reported in Journal of Applied Psychology and Personnel Psychology from 1980 to 2010 to produce empirical effect size benchmarks at the omnibus level, for 20 common research domains, and for an even finer grained level of generality. Results indicate that the usual interpretation and classification of effect sizes as small, medium, and large bear almost no resemblance to findings in the field, because distributions of effect sizes exhibit tertile partitions at values approximately one-half to one-third those intuited by Cohen (1988). Our results offer information that can be used for research planning and design purposes, such as producing better informed non-nil hypotheses and estimating statistical power and planning sample size accordingly. We also offer information useful for understanding the relative importance of the effect sizes found in a particular study in relationship to others and which research domains have advanced more or less, given that larger effect sizes indicate a better understanding of a phenomenon. Also, our study offers information about research domains for which the investigation of moderating effects may be more fruitful and provide information that is likely to facilitate the implementation of Bayesian analysis. Finally, our study offers information that practitioners can use to evaluate the relative effectiveness of various types of interventions.
-
Gignac, G. E., & Szodorai, E. T. (2016). Effect size guidelines for individual differences researchers. Personality and individual differences, 102, 74-78.
Individual differences researchers very commonly report Pearson correlations between their variables of interest. Cohen (1988) provided guidelines for the purposes of interpreting the magnitude of a correlation, as well as estimating power. Specifically, r = 0.10, r = 0.30, and r = 0.50 were recommended to be considered small, medium, and large in magnitude, respectively. However, Cohen’s effect size guidelines were based principally upon an essentially qualitative impression, rather than a systematic, quantitative analysis of data. Consequently, the purpose of this investigation was to develop a large sample of previously published meta-analytically derived correlations which would allow for an evaluation of Cohen’s guidelines from an empirical perspective. Based on 708 meta-analytically derived correlations, the 25th, 50th, and 75th percentiles corresponded to correlations of 0.11, 0.19, and 0.29, respectively. Based on the results, it is suggested that Cohen’s correlation guidelines are too exigent, as <3% of correlations in the literature were found to be as large as r = 0.50. Consequently, in the absence of any other information, individual differences researchers are recommended to consider correlations of 0.10, 0.20, and 0.30 as relatively small, typical, and relatively large, in the context of a power analysis, as well as the interpretation of statistical results from a normative perspective.
-
Paterson, T. A., Harms, P. D., Steel, P., & Credé, M. (2016). An assessment of the magnitude of effect sizes: Evidence from 30 years of meta-analysis in management. Journal of Leadership & Organizational Studies, 23(1), 66-81.
This study compiles information from more than 250 meta-analyses conducted over the past 30 years to assess the magnitude of reported effect sizes in the organizational behavior (OB)/human resources (HR) literatures. Our analysis revealed an average uncorrected effect of r = .227 and an average corrected effect of ρ = .278 (SDρ = .140). Based on the distribution of effect sizes we report, Cohen’s effect size benchmarks are not appropriate for use in OB/HR research as they overestimate the actual breakpoints between small, medium, and large effects. We also assessed the average statistical power reported in meta-analytic conclusions and found substantial evidence that the majority of primary studies in the management literature are statistically underpowered. Finally, we investigated the impact of the file drawer problem in meta-analyses and our findings indicate that the file drawer problem is not a significant concern for meta-analysts. We conclude by discussing various implications of this study for OB/HR researchers.
- Lovakov, A., & Agadullina, E. (2017). Empirically derived guidelines for interpreting effect size in social psychology. PsyArxiv
A number of recent research publications have shown that commonly used guidelines for interpreting effect sizes suggested by Cohen (1988) do not fit well with the empirical distribution of those effect sizes, and tend to overestimate them in many research areas. This study proposes empirically derived guidelines for interpreting effect sizes for research in social psychology, based on analysis of the true distributions of the two types of effect size measures widely used in social psychology (correlation coefficient and standardized mean differences). Analysis was carried out on the empirical distribution of 9884 correlation coefficients and 3580 Hedges’ g statistics extracted from studies included in 98 published meta-analyses. The analysis reveals that the 25th, 50th, and 75th percentiles corresponded to correlation coefficients values of 0.12, 0.25, and 0.42 and to Hedges’ g values of 0.15, 0.38, and 0.69, respectively. This suggests that Cohen’s guidelines tend to overestimate medium and large effect sizes. It is recommended that correlation coefficients of 0.10, 0.25, and 0.40 and Hedges’ g of 0.15, 0.40, and 0.70 should be interpreted as small, medium, and large effects for studies in social psychology. The analysis also shows that more than half of all studies lack sufficient sample size to detect a medium effect. This paper reports the sample sizes required to achieve appropriate statistical power for the identification of small, medium, and large effects. This can be used for performing appropriately powered future studies when information about exact effect size is not available.
-
Fryer Jr, R. G. (2017). The production of human capital in developed countries: Evidence from 196 randomized field experiments. In Handbook of economic field experiments (Vol. 2, pp. 95-322). North-Holland. Ungated
Randomized field experiments designed to better understand the production of human capital have increased exponentially over the past several decades. This chapter summarizes what we have learned about various partial derivatives of the human capital production function, what important partial derivatives are left to be estimated, and what—together—our collective efforts have taught us about how to produce human capital in developed countries. The chapter concludes with a back of the envelope simulation of how much of the racial wage gap in America might be accounted for if human capital policy focused on best practices gleaned from randomized field experiments.
[He split results by various groups, so hard to summarize]
-
Nuijten, M. B., van Assen, M. A., Augusteijn, H., Crompvoets, E. A. V., & Wicherts, J. (2018). Effect sizes, power, and biases in intelligence research: A meta-meta-analysis. PsyArxiv
In this meta-study, we analyzed 2,442 effect sizes from 131 meta-analyses in intelligence research, published from 1984 to 2014, to estimate the average effect size, median power, and evidence for bias in this multidisciplinary field. We found that the average effect size in intelligence research was a Pearson’s correlation of .26, and the median sample size was 60. We estimated the power of each primary study by using the corresponding meta-analytic effect as a proxy for the true effect. The median estimated power across all studies was 51.7%, with only 31.7% of the studies reaching a power of 80% or higher. We documented differences in average effect size and median estimated power between different types of in intelligence studies (correlational studies, studies of group differences, experiments, toxicology, and behavior genetics). Across all meta-analyses, we found evidence for small study effects, potentially indicating publication bias and overestimated effects. We found no differences in small study effects between different study types. We also found no convincing evidence for the decline effect, US effect, or citation bias across meta-analyses. We conclude that intelligence research does show signs of low power and publication bias, but that these problems seem less severe than in many other scientific fields.
-
Rubio-Aparicio, M., Marin-Martinez, F., Sanchez-Meca, J., & Lopez-Lopez, J. A. (2018). A methodological review of meta-analyses of the effectiveness of clinical psychology treatments. Behavior Research Methods, 50(5), 2057-2073.
This article presents a methodological review of 54 meta-analyses of the effectiveness of clinical psychological treatments, using standardized mean differences as the effect size index. We statistically analyzed the distribution of the number of studies of the meta-analyses, the distribution of the sample sizes in the studies of each meta-analysis, the distribution of the effect sizes in each of the meta-analyses, the distribution of the between-studies variance values, and the Pearson correlations between effect size and sample size in each meta-analysis. The results are presented as a function of the type of standardized mean difference: posttest standardized mean difference, standardized mean change from pretest to posttest, and standardized mean change difference between groups. These findings will help researchers design future Monte Carlo and theoretical studies on the performance of meta-analytic procedures, based on the manipulation of realistic model assumptions and parameters of the meta-analyses. Furthermore, the analysis of the distribution of the mean effect sizes through the meta-analyses provides a specific guide for the interpretation of the clinical significance of the different types of standardized mean differences within the field of the evaluation of clinical psychological interventions.
-
Brydges, C. R. (2019). Effect Size Guidelines, Sample Size Calculations, and Statistical Power in Gerontology. Innovation in aging, 3(4), igz036.
Researchers typically use Cohen’s guidelines of Pearson’s r = .10, .30, and .50, and Cohen’s d = 0.20, 0.50, and 0.80 to interpret observed effect sizes as small, medium, or large, respectively. However, these guidelines were not based on quantitative estimates and are only recommended if field-specific estimates are unknown. This study investigated the distribution of effect sizes in both individual differences research and group differences research in gerontology to provide estimates of effect sizes in the field. Effect sizes (Pearson’s r, Cohen’s d, and Hedges’ g) were extracted from meta-analyses published in 10 top-ranked gerontology journals. The 25th, 50th, and 75th percentile ranks were calculated for Pearson’s r (individual differences) and Cohen’s d or Hedges’ g (group differences) values as indicators of small, medium, and large effects. A priori power analyses were conducted for sample size calculations given the observed effect size estimates. Effect sizes of Pearson’s r = .12, .20, and .32 for individual differences research and Hedges’ g = 0.16, 0.38, and 0.76 for group differences research were interpreted as small, medium, and large effects in gerontology. Cohen’s guidelines appear to overestimate effect sizes in gerontology. Researchers are encouraged to use Pearson’s r = .10, .20, and .30, and Cohen’s d or Hedges’ g = 0.15, 0.40, and 0.75 to interpret small, medium, and large effects in gerontology, and recruit larger samples.
- Lortie-Forgues, H., & Inglis, M. (2019). Rigorous large-scale educational RCTs are often uninformative: Should we be concerned?. Educational Researcher, 48(3), 158-166.
There are a growing number of large-scale educational randomized controlled trials (RCTs). Considering their expense, it is important to reflect on the effectiveness of this approach. We assessed the magnitude and precision of effects found in those large-scale RCTs commissioned by the UK-based Education Endowment Foundation and the U.S.-based National Center for Educational Evaluation and Regional Assistance, which evaluated interventions aimed at improving academic achievement in K–12 (141 RCTs; 1,222,024 students). The mean effect size was 0.06 standard deviations. These sat within relatively large confidence intervals (mean width = 0.30 SDs), which meant that the results were often uninformative (the median Bayes factor was 0.56). We argue that our field needs, as a priority, to understand why educational RCTs often find small and uninformative effects.
-
Schäfer, T., & Schwarz, M. (2019). The meaningfulness of effect sizes in psychological research: Differences between sub-disciplines and the impact of potential biases. Frontiers in Psychology, 10, 813.
Effect sizes are the currency of psychological research. They quantify the results of a study to answer the research question and are used to calculate statistical power. The interpretation of effect sizes—when is an effect small, medium, or large?—has been guided by the recommendations Jacob Cohen gave in his pioneering writings starting in 1962: Either compare an effect with the effects found in past research or use certain conventional benchmarks. The present analysis shows that neither of these recommendations is currently applicable. From past publications without pre-registration, 900 effects were randomly drawn and compared with 93 effects from publications with pre-registration, revealing a large difference: Effects from the former (median r = 0.36) were much larger than effects from the latter (median r = 0.16). That is, certain biases, such as publication bias or questionable research practices, have caused a dramatic inflation in published effects, making it difficult to compare an actual effect with the real population effects (as these are unknown). In addition, there were very large differences in the mean effects between psychological sub-disciplines and between different study designs, making it impossible to apply any global benchmarks. Many more pre-registered studies are needed in the future to derive a reliable picture of real population effects.