This is the sister post to the one on Anglo Reaction’s Substack. We published a new paper of high significance, and we didn’t agree about how to summarize it for a wider audience. So we decided to just post both on our respective blogs. Why not? There’s no censorship here, and no lack of space. For good measure, here’s a Twitter poll about which one is better.
Suppose you wanted to increase economic growth in your country. I know, in the times of ‘degrowth’ mania, you may be somewhat quaint to wish for more economic growth. BUT suppose you still wanted more economic growth, what should you do? Well, is there a science that deals with these matters that we can learn from? Yes, economics. What have they learned? Well, according to some economists: not much!
There is a literature on what is called “robust ambiguity”, meaning that different methods give different answers about what really promotes economic growth, and so the right position is to throw the arms up in the air and say we don’t know. In contrast to this view, one might take a more standard approach. Don’t free markets promote economic growth? Many people have heard of the miracle of Chile, and that seems hard to explain away (sadly Chile is now turning to socialism again). And what about being poor to begin with? Granted, not all poor countries grow fast, but a lot of countries that grew very fast in the last couple of decades were poor to begin with, called the advantage of backwardness. That’s certainly true for the Asian tigers, and the Big Tiger is also growing very well since it too gave up on socialism (sort of). Going further, people familiar with intelligence research will know of findings going back a few decades that national intelligence, whichever way you measure them, predicts economic growth fairly well. What about that? Have mainstream economists not examined this? Or have they examined it and found it wanting?
Setting that question aside for now, think about the statistics of the issue. There are only 200ish countries in the world. Not all of these have available data for economic growth going back decades, usually because they are too poor or war-torn or corrupt to collect accurate government statistics. So these countries cannot be easily used in studies, as one has to fill in the missing data with guesses. And what about all the things that people have claimed cause or at least predict economic growth? There’s probably several hundred such factors that have been claimed and supporter in one study somewhere. Is there a way to do a big master-study that examines them at all once and gives us a clear answer?
Well, yes and no. The no answer is that you cannot plug all of the predictors into a single regression model and get reliable answers. It’s simply a matter of statistics: you have more predictors than countries, and so the model cannot fit. OK, you could fit it using penalization (ridge/lasso/net), but this will come at a cost of more bias. Though you can’t fit a full model, you could fit some subsets, i.e., pick some of the variables by your judgement call and present those models. There are 1000s of studies of economic growth, each using different measures of GDP, different sets of countries, different sets of controls to achieve their beloved p < .05. A lot of this is just plain cheating. They tried a lot of ways to fit a model until they found one that ‘worked’. There is a smart way to get around both of these problems: Bayesian Model Averaging (BMA). The idea is to fit a lot of models without cheating. Millions of models in fact. If you have 200 predictors, there are 2^200 possible models, which is like a lot. You can’t fit all of those, as that would take approximately forever. But fortunately, you can pick at random from this population of models and try out, say, 5 million of them. Then you rank these models by their ‘model fit’ (R², BIC etc.), and then take a weighted mean of the best 1000 models. That is essentially what BMA does for you. Using the results from the 5 million models you fit, you could see the performance of a given predictor. Does it work well regardless of which other predictors are in the model? Does it always have the same sign i.e. direction of effect? Is it always found in the best models? If the answer to these questions is “yes yes yes”, then you have found a robust predictor.
So, what the robust ambiguity supporters are saying is that they tried this approach and they found that nothing is robust. If one does the modeling one way, one gets one answer; if one does it another, one gets a different answer. Unsatisfactory. However, there is a catch. These people have been ignoring national intelligence in their BMA studies. That is, except for ONE paper. In 2006, Garett Jones and W. J. Schneider published this important paper:
- Jones, G., & Schneider, W. J. (2006). Intelligence, human capital, and economic growth: A Bayesian averaging of classical estimates (BACE) approach. Journal of economic growth, 11(1), 71-93.
Human capital plays an important role in the theory of economic growth, but it has been difficult to measure this abstract concept. We survey the psychological literature on cross-cultural IQ tests and conclude that intelligence tests provide one useful measure of human capital. Using a new database of national average IQ, we show that in growth regressions that include only robust control variables, IQ is statistically significant in 99.8% of these 1330 regressions, easily passing a Bayesian model-averaging robustness test. A 1 point increase in a nation’s average IQ is associated with a persistent 0.11% annual increase in GDP per capita.
2006 was 16 years ago, so why haven’t the following BMA studies tried this approach again? We can’t say for sure, but you probably know the answer. National intelligence is controversial. It can get your nice paper retracted if you are unlucky enough. So why go there if you are looking for a nice career? Alternatively, most economists have simply not heard of this approach. Economics is kinda insular, and there isn’t much overlap with intelligence research, which is odd. Whatever the reason, we sought to find out whether the robustness skeptics are right, or whether national intelligence can pass the muster. The result is this 72 page behemoth that is just published:
- Francis, G., & Kirkegaard, E. O. W. (2022). National Intelligence and Economic Growth: A Bayesian Update. Mankind Quarterly, 63(1), Article 2. https://doi.org/10.46469/mq.2022.63.1.2
Since Lynn and Vanhanen’s book IQ and the Wealth of Nations (2002), many publications have evidenced a relationship between national IQ and national prosperity. The strongest statistical case for this lies in Jones and Schneider’s (2006) use of Bayesian model averaging to run thousands of regressions on GDP growth (1960-1996), using different combinations of explanatory variables. This generated a weighted average over many regressions to create estimates robust to the problem of model uncertainty. We replicate and extend Jones and Schneider’s work with many new robustness tests, including new variables, different time periods, different priors and different estimates of average national intelligence. We find national IQ to be the “best predictor” of economic growth, with a higher average coefficient and average posterior inclusion probability than all other tested variables (over 67) in every test run. Our best estimates find a one point increase in IQ is associated with a 7.8% increase in GDP per capita, above Jones and Schneider’s estimate of 6.1%. We tested the causality of national IQs using three different instrumental variables: cranial capacity, ancestry-adjusted UV radiation, and 19th-century numeracy scores. We found little evidence for reverse causation, with only ancestry-adjusted UV radiation passing the Wu-Hausman test (p < .05) when the logarithm of GDP per capita in 1960 was used as the only control variable. Key Words: Human capital, National IQ, Economic growth, Bayesian model averaging, Intelligence, Smart fraction
We find that more or less no matter how we try the modeling, we always get the answer that national intelligence is a good and important predictor of economic growth. Robust ambiguity avoided! Rejoice, now we can go back to telling politicians that we need to increase our national intelligence (yes, that means the bad bad E word). Graphically, the results look like this:
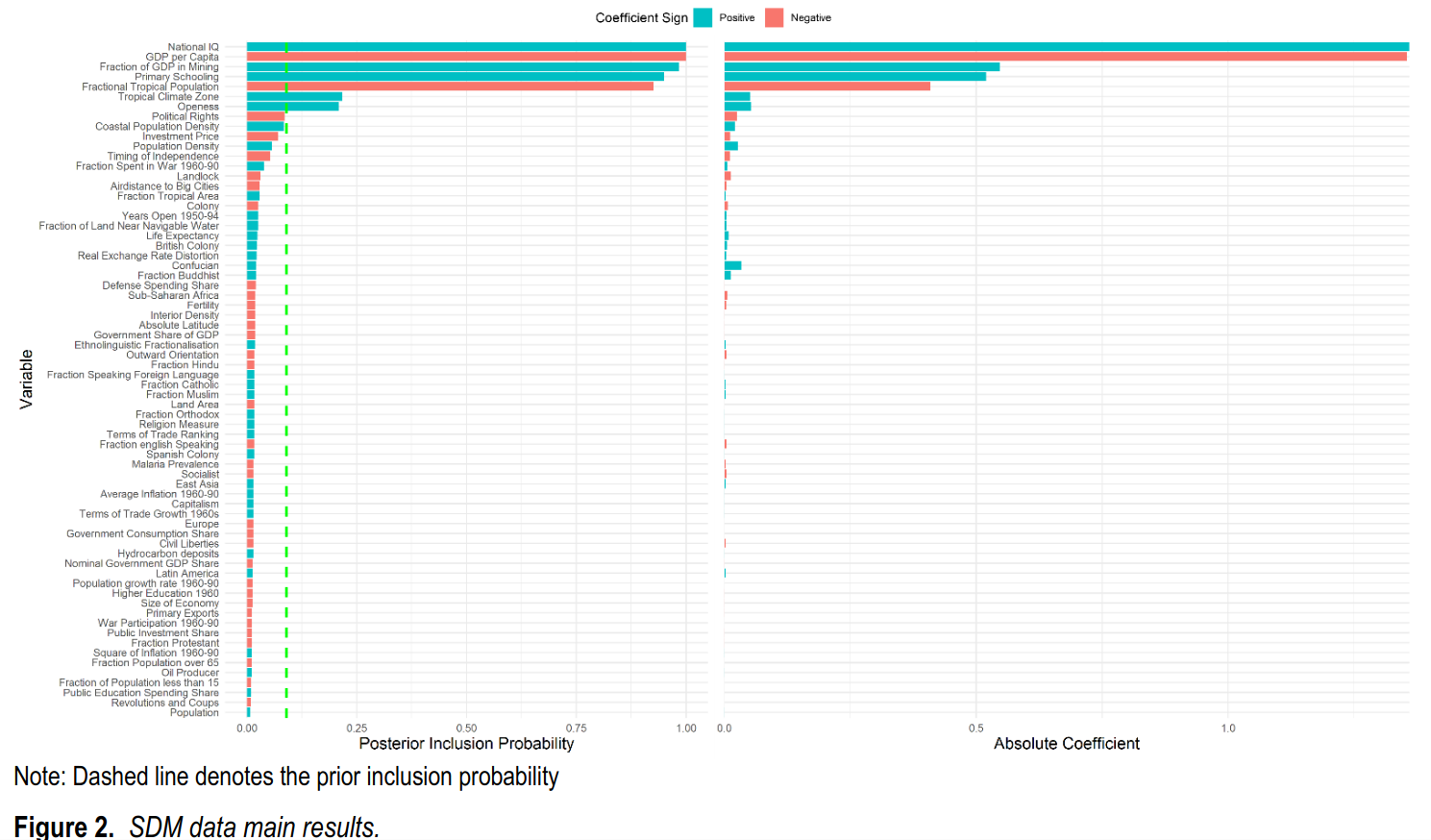
The left panel shows the probability that a given predictor was present in the best models (the PIP). 1.00 thus means 100%, it was always present. There’s only 2 variables that are always present. These are national IQ and GDP per capita in 1960. The latter variable is the advantage of backwardness mentioned above. The next predictor is natural resources in terms of mining. That one is basically just a matter of luck, and I guess not having environmentalist policies that prevent mining. Primary schooling enrollment also seems important. Being tropical is also a negative factor that seems important, but not much you can do about that aside from colonizing a new place to live, or maybe buying land.
The right panel shows the importance of the predictor, i.e., the standardized beta. Red color means it is negative, turquoise means positive, so you want a big turquoise bar. The biggest such bar is the one for national intelligence. That’s the best predictor.
Actually, this is just our first dataset. We used a second dataset compiled by different researchers to see if the results would be, well, robust:

The two most important predictors are the same as before. Starting out poor is good and being smart is good. This time there’s no mining but there’s a predictor called primary exports, which I guess covers the same thing, i.e., natural resources. There’s no primary schooling to see here, but now we see that life expectancy is good. The contrast between the two datasets illustrate what the critics have been saying, i.e., that varying the study design leads to different results (in this case, the base dataset). Well, we agree, but not as far as the two main predictors are concerned. National intelligence works every time pretty much. We tried a lot of method variations. We tried 1) different priors in the BMA settings (that’s the Bayesian part), 2) different national intelligence estimates (Lynn, Becker, Worldbank, Rindermann and more), 3) different estimates of GDP per capita to compute economic growth from, 4) two different datasets of control variables, 5) forcing some control variables to be in the models always instead of ‘playing fair’, 6) subsetting the data at random to look if outliers were responsible, and 7) looking at shorter time periods. We find that national intelligence does well across the board. No ambiguity here.
With regards to causality, it’s the usual debate. One easy approach is to use old national intelligence estimates. This can be done using Becker’s dataset, as one can simply exclude studies newer than a certain year. This is the approach of Christainsen’s 2020 study. However, we opted for another approach, namely the age heaping scores that one of us blogged about recently. We find that these work well too, despite being collected in the 1800s and early 1900s. Using instrumental variables, we also find support for causality, and it’s p < .001 across the board, not the usual p = .045 shenanigans that economists are known for.
On the negative side, we are unable to find much evidence for smart fraction theory, or economic freedom. These variables do not perform up to par in our analyses. This is awkward for me as I have another nice study in review that shows how well smart fraction theory works! My thinking is that BMA is a hard bar to pass. If a variable can be robust in this, it must be very good indeed. If it cannot be robust, but only shows some evidence, then it goes into the indeterminate category of variables that may have less importance but still worth caring about in future research. The sample size for BMA is not that large, about 70 countries. That’s due to the need for having data for all the control variables. It should be possible to expand the dataset to say 100 countries without dropping too many control variables, and then checking these secondary variables again.
Overall, quite the kickass paper, we hope you will enjoy it, now head over to George Francis’ version if you haven’t already.