New paper out: Global Ancestry and Cognitive Ability (PNC study)

Lasker, J., Pesta, B. J., Fuerst, J. G., & Kirkegaard, E. O. W. (2019). Global Ancestry and Cognitive Ability. Psych, 1(1), 431-459.

Using data from the Philadelphia Neurodevelopmental Cohort, we examined whether European ancestry predicted cognitive ability over and above both parental socioeconomic status (SES) and measures of eye, hair, and skin color. First, using multi-group confirmatory factor analysis, we verified that strict factorial invariance held between self-identified African and European-Americans. The differences between these groups, which were equivalent to 14.72 IQ points, were primarily (75.59%) due to difference in general cognitive ability (g), consistent with Spearman’s hypothesis. We found a relationship between European admixture and g. This relationship existed in samples of (a) self-identified monoracial African-Americans (B = 0.78, n = 2,179), (b) monoracial African and biracial African-European-Americans, with controls added for self-identified biracial status (B = 0.85, n = 2407), and (c) combined European, African-European, and African-American participants, with controls for self-identified race/ethnicity (B = 0.75, N = 7,273). Controlling for parental SES modestly attenuated these relationships whereas controlling for measures of skin, hair, and eye color did not. Next, we validated four sets of polygenic scores for educational attainment (eduPGS). MTAG, the multi-trait analysis of genome-wide association study (GWAS) eduPGS (based on 8442 overlapping variants) predicted g in both the monoracial African-American (r = 0.111, n = 2179, p < 0.001), and the European-American (r = 0.227, n = 4914, p < 0.001) subsamples. We also found large race differences for the means of eduPGS (d = 1.89). Using the ancestry-adjusted association between MTAG eduPGS and g from the monoracial African-American sample as an estimate of the transracially unbiased validity of eduPGS (B = 0.124), the results suggest that as much as 20%–25% of the race difference in g can be naïvely explained by known cognitive ability-related variants. Moreover, path analysis showed that the eduPGS substantially mediated associations between cognitive ability and European ancestry in the African-American sample. Subtest differences, together with the effects of both ancestry and eduPGS, had near-identity with subtest g-loadings. This finding confirmed a Jensen effect acting on ancestry-related differences. Finally, we confirmed measurement invariance along the full range of European ancestry in the combined sample using local structural equation modeling. Results converge on genetics as a potential partial explanation for group mean differences in intelligence.

This is our largest admixture project to date, pulling together the evidence using polygenic scores and global admixture analysis (see previous posts). We confirm all the usual hereditarian predictions using a large sample of European and African American kids and youth from the PNC/TCP sample. The dataset also has other groups, mainly about 500 Hispanics, but we left these out to simplify the analysis and its presentation. Many people found our previous PING study hard to understand, so we felt this was needed. Specifically, we showed that:

Measurement issues can be analyzed with both Jensen’s method (correlated vectors) and MGCFA, and they give similar results, i.e. lack of notable bias. Table 1 shows MGCFA results. We have more work coming out on this question with the same conclusion but more in depth item-based methods.
In line with previous Jensen method findings, we show that there is a positive manifold among the tests: higher g-loadings, heritability, group gaps (genetic measured or not) etc., all relate positively. Table 14 shows these results.
Genetic ancestry (based on DNA) predicts intelligence in the way expected based on the hereditarian model. This predictive power doesn’t go entirely away if one controls for parental education, own skin color, or (current) polygenic scores. Results shown in Tables 4-8, 10-13, Figures 3-5.
Polygenic scores for education/IQ works for both European and African descent people in the PNC. It works better for the European ones, as expected, but about half the validity is retained in the Africans. This makes them a biased genetic measure but not a useless one. We show using this that the PGS mediates some of the ancestry effect, a prediction from the hereditarian model. A perfect PGS is expected to completely mediate the predictive power of genetic ancestry, so we expect as stronger GWASs are published, this will increasingly occur. In fact, we should have shown this by using the older GWASs. Results in Table 8 and Figure 4.

For a good quantitative background on understanding the results, I recommend reading the simulations we published in the PING paper supplement. It goes over why we modeled the data in this way since we simulated polygenic group differences and admixture analysis from first principles and showed the methods make sense. If you want the R code for that to play with it yourself, it can be found here.

Coverage by others:

Reddit threads: r/heredity
Inductivist: Blockbuster study on the black-white gap in intelligence
Steve Sailer: “Global Ancestry and Cognitive Ability”, also on VDare

Main figures and tables:

Table 1. Factor score differences between African and European-Americans based on the Weak Spearman’s Hypothesis Model.

Factor	Estimate	SE	Lower 95% CI	Upper 95% CI
g	1.046	0.020	1.007	1.085
Complex Reasoning	0.356	0.026	0.305	0.407
Executive Functioning	−0.055	0.028	−0.109	−0.0001
Episodic Memory	0	–	–	–

—

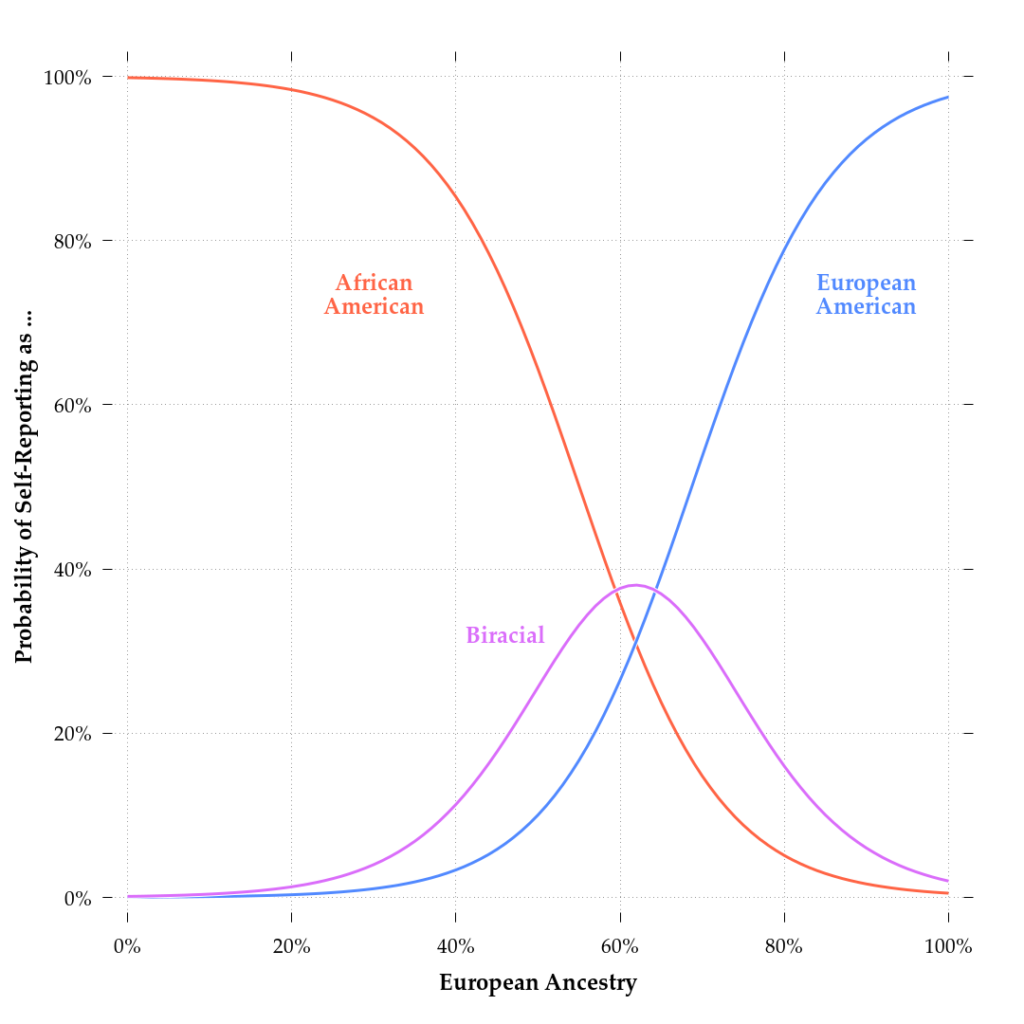
Figure 1. Probability distribution for identifying as African-, biracial African-European, and European-American as a function of genetic ancestry for the Trajectories of Complex Phenotypes (TCP) sample.

—

Figure 2. Regression plot of the relation between color (with higher values indicating darker color) and European genetic ancestry.

—

Table 2. Sample characteristics for the African, European, and biracial African-European-American participants.

	Age (SD; N)	% European (SD; N)	Mean SES (SD; N)	Mean g Score (SD; N)	Mean Color (SD; N)
African	14.08 (3.75; 2227)	0.187 (0.117; 2228)	−0.57 (0.77; 2180)	−1.01 (1.07; 2179)	30.96 (5.87; 1557)
Biracial African-European	13.15 (3.58; 232)	0.796 (0.289; 232)	0.16 (0.95; 230)	−0.14 (1.05; 228)	19.18 (7.61; 166)
European	13.76 (3.64; 4937)	0.986 (0.059; 4939)	0.33 (0.96; 4909)	0.00 (1.01; 4914)	14.70 (3.84; 3862)

Note: Standard deviations and sample sizes appear in parentheses. SES = socioeconomic status.

—

Table 3. Pairwise correlations among African-, African-European, and European-Americans.

	Cognitive Ability	SES	Euro. Ancestry	Afr. Ancestry	SIRE EA	SIRE AA	Color	EduPGS
Cognitive Ability	1
SES	0.406 (7253)	1
European Ancestry	0.411 (7321)	0.412 (7319)	1
African Ancestry	−0.411 (7321)	−0.412 (7319)	−1.000 (7399)	1
SIRE EA	0.408 (7321)	0.413 (7319)	0.964 (7399)	−0.964 (7399)	1
SIRE AA	−0.387 (7321)	−0.395 (7319)	−0.928 (7399)	0.928 (7399)	-0.930 (7399)	1
Color	−0.359 (5534)	−0.354 (5530)	−0.875 (5585)	0.875 (5585)	−0.838 (5585)	0.812 (5585)	1
EduPGS	0.402 (7321)	0.445 (7319)	0.672 (7399)	−0.672 (7399)	0.645 (7399)	−0.630 (7399)	−0.614 (7399)	1

Note: All values significant at p < 0.0001. Pairwise N in parentheses. SES = socioeconomic status, SIRE = self-identified race/ethnicity, eduPGS = education polygenic score.

—

Table 4. Pairwise correlations among self-identified monoracial African-American (below the diagonal) and self-identified monoracial and biracial African-European-American (above the diagonal).

	Cognitive Ability	SES	Euro. Ancestry	Afro. Ancestry	Color	EduPGS
Cognitive Ability	1	0.315 * (2367)	0.251 * (2407)	−0.251 * (2407)	−0.188 * (1690)	0.212 * (2407)
SES	0.256 * (2140)	1	0.276 * (2410)	−0.276 * (2410)	−0.184 * (1690)	0.244 * (2410)
European Ancestry	0.086 * (2179)	0.054 * (2180)	1	−1.000 * (2460)	−0.639 * (1723)	0.522 * (2460)
African Ancestry	−0.086 * (2179)	−0.054 * (2180)	−1.000 * (1854)	1	0.639 * (1723)	−0.522 * (2460)
Color	−0.084 * (1526)	−0.047 (1524)	−0.389 * (1557)	0.389 * (1557)	1	−0.394 * (1723)
EduPGS	0.112 * (2179)	0.119 * (2180)	0.328 * (2228)	−0.328 * (2228)	−0.187 * (1557)	1

Note: * Significant at p < 0.01. Pairwise N in parentheses. SES = socioeconomic status, eduPGS = education polygenic score.

—

Table 5. Regression analysis for European ancestry as a predictor of g among monoracial African-Americans with controls for skin color (Model 2), and SES (Model 3) added.

	Model 1			Model 1b			Model 2			Model 3
Predictor	B	SE	β	B	SE	β	B	SE	β	B	SE	β
Intercept	−1.16	0.04	−1.01	−0.82	0.06	−0.997	−1.05	0.09	−0.996	−0.83	0.09	−0.995
EUR	0.78 ***	0.19	0.09 ***				0.83 ***	0.24	0.10 ***	0.67 **	0.23	0.08 **
Skin Color				−0.13 ***	0.04	−0.09 ***	−0.07	0.04	−0.05	−0.06	0.04	−0.04
SES										0.36 ***	0.03	0.28 ***
Adjusted R²	0.007			0.006			0.013			0.082
N	2179			1526			1526			1500

Note: * p < 0.05, ** p < 0.01, *** p < 0.001. Model 1b shows the results with color as an alternative predictor. EUR = European ancestry. SES = socioeconomic status.

—

Table 6. Regression analysis for European ancestry as a predictor of g among monoracial and biracial African-European-Americans with controls for SIRE (Model 2), skin color (Model 3b), and SES (Model 4) added.

	Model 1		Model 2		Model 3a		Model 3b		Model 4
Predictor	B	SE	B	SE	B	SE	B	SE	B	SE
Intercept	−1.22	0.03	−1.17	0.04	−0.62	0.05	−1.07	0.08	−0.83	0.08
EUR	1.21 ***	0.09	0.85 ***	0.15			0.80 ***	0.19	0.55 **	0.19
SIRE: EA			0.35 **	0.12			0.27 *	0.13	0.18	0.13
Skin Color					−0.25 ***	0.03	−0.06	0.04	−0.05	0.04
SES									0.37	0.03
Adjusted R²	0.063		0.066		0.035		0.065		0.134
N	2407		2407		1690		1690		1664

Note: * p < 0.05, ** p < 0.01, *** p < 0.001. EUR = European ancestry. SES = socioeconomic status, SIRE = self-identified race/ethnicity.

—

Figure 3. Regression plot for the relation between g and European ancestry (r = 0.411).

—

Table 7. Regression analysis for European ancestry as a predictor of g among African-, European-, and biracial African-European-Americans with controls for SIRE (Model 2) skin color (Model 3), and SES (Model 4) Added.

	Model 1		Model 2		Model 3a		Model 3b		Model 4
Predictor	B	SE	B	SE	B	SE	B	SE	B	SE
Intercept	−1.22	0.03	−1.15	0.09	−0.28	0.01	−1.09	0.11	−0.91	0.11
EUR	1.23 ***	0.03	0.75 ***	0.13			0.74 ***	0.16	0.59 ***	0.15
SIRE: EA			0.41 ***	0.11			0.35 **	0.12	0.22 *	0.11
SIRE: AA			0.00	0.08			−0.02	0.09	0.01	0.08
Skin Color					−0.40 ***	0.01	−0.02	0.03	−0.01	0.03
SES									0.34 ***	0.01
Adjusted R²	0.169		0.170		0.129		0.166		0.238
N	7321		7321		5534		5534		5488

Note: * p < 0.05, ** p < 0.01, *** p < 0.001. EUR = European ancestry. SES = socioeconomic status, SIRE = self-identified race/ethnicity.

—

Table 8. Pairwise correlations between cognitive ability and education/intelligence-related polygenic scores (European-American above the diagonal, African-American below).

	Cognitive Ability	Putative Causal	GWAS_edu PGS	MTAG_10K_eduPGS	MTAG_Lead eduPGS
Cognitive Ability	1	0.058 *** (4914)	0.225 *** (4914)	0.227 *** (4914)	0.210 *** (4914)
Putative Causal_edu PGS	0.031 (2179)	1	0.216 *** (4939)	0.315 *** (4939)	0.348 *** (4939)
GWAS_edu PGS	0.044 * (2179)	0.135 *** (2228)	1	0.645 *** (4939)	0.574 *** (4939)
MTAG_10K_eduPGS	0.112 *** (2179)	0.228 *** (2228)	0.484 *** (2228)	1	0.837 *** (4939)
MTAG_Lead_PGS	0.094 *** (2179)	0.266 *** (2228)	0.453 *** (2228)	0.801 *** (2228)	1

Note: * Significant at p < 0.05; ** Significant at p < 0.01; *** Significant at p < 0.001. N in parentheses. GWAS = genome-wide association study (standard one-at-a-time regression), MTAG = multi-trait analysis of GWAS, eduPGS = education polygenic score, lead = genome wide-

—

Figure 4. Regression plot for the predictive validity of MTAG 10k eduPGS with Respect to g in the African-American (Red; r = 0.112) and European-American (Blue; r = 0.227) Samples.

—

Table 9. Mean racial differences in eduPGS (MTAG_10k).

	N	M	SD
European-American	4939	0.00	1.00
Biracial African-European-American	232	−0.59	1.15
African-American	2228	−1.79	0.81

—

Table 10. Regression results for the effect of eduPGS on cognitive ability among monoracial African-Americans.

	Model 1b		Model 2b
Predictor	B	SE	B	SE
Intercept	−0.88	0.08	−0.75	0.12
EUR	0.50 *	0.21	0.51 *	0.25
eduPGS	0.12 ***	0.03	0.13 ***	0.04
Color			−0.07	0.04
Adjusted R²	0.014		0.021
N	2179		1526

Note: * p < 0.05, ** p < 0.01, *** p < 0.001. EUR = European ancestry. eduPGS = education polygenic score.

—

Table 11. Regression results for the effect of eduPGS on cognitive ability among African, biracial African-European, and European-Americans.

	Model 1b		Model 2b
Predictor	B	SE	B	SE
Intercept	−0.73	0.09	−0.64	0.12
EUR	0.29 *	0.13	0.27	0.16
SIRE: EA	0.44 ***	0.10	0.37 **	0.11
SIRE: AA	0.04	0.07	0.01	0.09
eduPGS	0.21 ***	0.01	0.20 ***	0.01
Color			−0.01	0.03
Adjusted R²	0.200		0.196
N	7321		5534

Note: * p < 0.05, ** p < 0.01, *** p < 0.001. EUR = European ancestry. SES = socioeconomic status, SIRE = self-identified race/ethnicity, eduPGS = education polygenic score.

—

Table 12. Regression results for the effect of eduPGS on cognitive ability among European-Americans.

	Model 1		Model 2		Model 3
Predictor	B	SE	B	SE	B	SE
Intercept	−0.45	0.25	0.02	0.24	−0.03	0.27
EUR	0.45	0.25	−0.02	0.24	0.04	0.28
eduPGS			0.23 ***	0.01	0.22 ***	0.02
Color					0.02	0.04
Adjusted R²	0.000		0.051		0.50
N	4914		4914		3844

Note: * p < 0.05, ** p < 0.01, ** p < 0.001. EUR = European ancestry. SES = socioeconomic status, SIRE = self-identified race/ethnicity, eduPGS = education polygenic score.

—

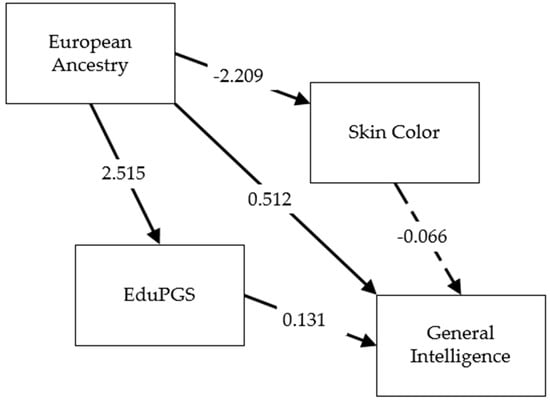
Figure 5. Path diagram for relation between European Ancestry, color, eduPGS, and g in the African-American sample.

—

Table 13. Detailed results for path diagram.

			Unstandardized Estimate	S.E.	P value	Lower 95% CI	Upper 95% CI	Standardized Estimate
EUR	➜	G	0.512	0.255	0.045	0.013	1.012	0.059
EUR	➜	eduPGS	2.515	0.156	0.000	2.209	2.821	0.381
eduPGS	➜	G	0.131	0.036	0.000	0.060	0.202	0.099
Skin Color	➜	G	−0.066	0.043	0.120	−0.150	0.017	0.043
EUR	➜	Skin Color	−2.209	0.133	0.000	−2.469	−1.949	−0.392
Skin Color	~	eduPGS	−0.020	0.012	0.089	−0.044	0.003	−0.044

Note: EUR = European ancestry.

—

Table 14. Results from Jensen’s Method of Correlated Vectors.

	g Loading	B-W h²	Ancestry r	eduPGS r (European-American)	eduPGS r (African American)	African/European Gap
g loading	1
B-W h²	0.372	1
Ancestry r	0.941	0.467	1
eduPGS r (European-American)	0.892	0.604	0.993	1
eduPGS r (African-American)	0.901	0.600	0.836	0.846	1
African/European gap	0.929	0.478	0.997	0.926	0.813	1

Note: N (subtest) = 10. eduPGS = education polygenic score, h² = heritability.

You Might Also Like

Comment on CPGGrey’s new video on the future of automatization

Editor Matthias Ziegler rejects paper for political reasons, then says science should be neutral

The g factor and principal components regression

Leave a Reply Cancel reply